光照

SunSolve Power 允许用户定义一个或多个光照源。这些光照源用于将光学求解器得到的、随波长变化的吸收率、反射率和透射率转换为标量量，例如等效光子电流密度。最终结果通过对所有已定义光源的贡献进行积分得到。

需要注意的是，所选光谱并不决定求解所覆盖的波长范围；波长范围需在“Options”标签页中单独设置。

位置

每个光照源的作用区域可以设置为“full area”或“defined”。

定义区域（defined-area）的光照源可以是圆形（如下图所示），其直径由用户指定；也可以是矩形，其宽度和长度由用户指定。局部光照在电池（或组件）上的位置则由 $x_{\text{offset}}$ 和 $y_{\text{offset}}$ 定义，如图所示，这两个参数表示从电池（或组件）中心到局部光照中心的距离。

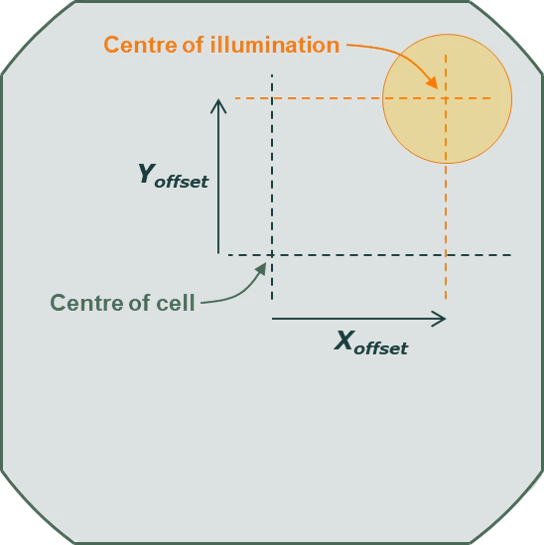
如果局部光照的一部分并未覆盖电池（或组件），则这部分光照不会与电池（或组件）发生任何相互作用。它既不会被计入透射光分量，而是归类为“remainder”（剩余部分）。

施加局部光照有助于分析电池或组件中特定区域的行为，例如，带纹理的焊带捕获的光的比例，或电池之间背板区域捕获的光的比例。

角分布

角分布有三种选项：

1. Single angle：用户通过天顶角和方位角来定义光线方向。该角分布可以视为一个 delta 函数。
2. Isotropic：天顶角具有 sin θ 依赖。* 各向同性分布有时用于表示漫射日光。它等效于具有均匀辐射强度（每单位立体角的强度恒定）。
3. Gaussian：天顶角服从 exp[–θ²/(2σ²)] 形式的高斯分布（即以 θ = 0 为中心的高斯函数）。这可以用来表示电池测试仪中平面扩散板产生的光照，该光照名义上为法向入射，但实际上具有一定的小角度发散。

在水平平面上的相对辐照度 ξ 为：

1. ξ = ʃcos θ∙δ(θ)∙dθ / ʃδ(θ)∙dθ = cos Θ，其中 Θ 为用户设定的天顶角；
2. ξ = ʃcos θ∙sin θ∙dθ / ʃsin θ∙dθ = 1/2；
3. ξ = ʃcos θ∙exp[–θ²/(2σ²)]∙dθ / ʃexp[–θ²/(2σ²)]∙dθ，当 σ 很小时趋近于 1，当 σ 很大时趋近于 2/π；

其中积分上下限为 θ = 0 和 π/2。

光谱与入射强度

所选光谱的光谱强度 $I_b(\lambda)$ 被假定为垂直平面上的入射光束强度，单位为 W/m²/nm。因此，在给定波长范围内对光谱强度积分即可得到垂直平面上的光束强度 $\Phi_b$（单位 W/m²）。

可以通过设置缩放因子 $f$ 来整体缩放该强度。该因子会在所有波长上等比例缩放 $I_b(\lambda)$。

水平平面上的辐照度因此为 $\Phi_h = \xi \cdot f \cdot \Phi_b$。

我们将前因子 ξ∙f 称为相对水平辐照度（relative horizontal irradiance, RHI），并在每个光照源的输出中给出。

下面通过三个示例说明应如何上传实测光谱。在每个示例中，光谱强度 $I_m(\lambda)$ 均是在水平平面上测得。我们建议在上传前先将 $I_m(\lambda)$ 乘以 1/ξ 得到 $I_b(\lambda)$，这样就无需再修改缩放因子 $f$。

示例 1：在太阳天顶角为 30° 时，在水平平面上测量直射太阳光谱。上传前先将 $I_m(\lambda)$ 乘以 1/cos(30°) = 1.154 得到 $I_b(\lambda)$，然后将 $I_b(\lambda)$ 作为新的自定义光谱上传。

示例 2：在水平平面上测量漫天空辐照度光谱。这种情况很常见，因为许多 DHI（漫射水平辐照度）测量是通过水平安装的辐射表完成的。如果假设光照为各向同性（朗伯），则 ξ = 1/2，应将 $I_m(\lambda)$ 乘以 2 得到 $I_b(\lambda)$，再将 $I_b(\lambda)$ 作为自定义光谱上传。

示例 3：测量某电池测试仪在水平平面上的辐照度，而已知该测试仪的角分布为 σ = 10° 的高斯分布。上传前先将 $I_m(\lambda)$ 乘以 1/ξ = 1.015 得到 $I_b(\lambda)$，然后上传 $I_b(\lambda)$ 作为新的自定义光谱。

在上述所有示例中，我们都建议先将实测光谱 $I_m(\lambda)$ 乘以 1/ξ 转换为 $I_b(\lambda)$ 后再上传。此时可以保持缩放因子 $f = 1$。另一种做法是直接将 $I_m(\lambda)$ 作为自定义光谱上传，并将缩放因子设为 $f = 1/\xi$（这样得到的相对水平辐照度为 1）。

光照源的坐标系

用于定义光照源方向的坐标系取决于仿真的配置：

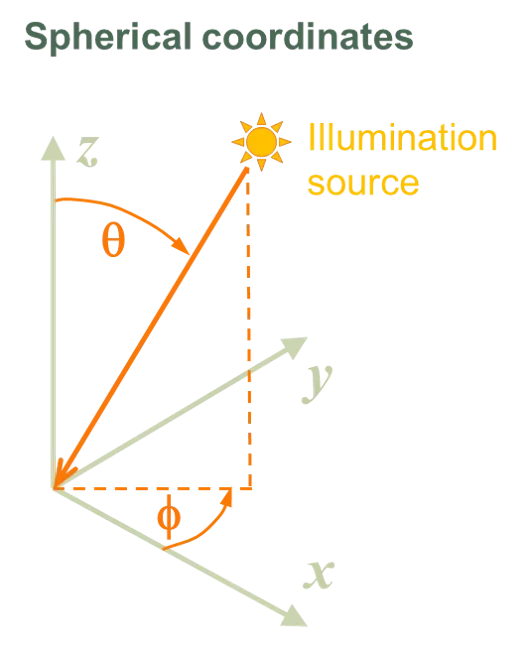
• 当仿真对象为太阳能电池或组件时，采用基于笛卡尔坐标的球坐标系。此时光照方向由天顶角 θ 和方位角 φ 定义。
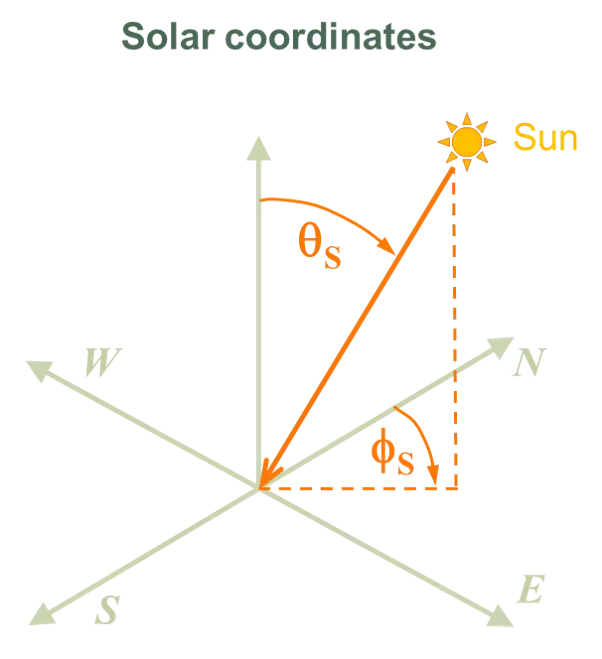
• 当仿真对象为系统时，采用基于方位方向的太阳坐标系。此时太阳位置由太阳天顶角 $\theta_S$ 和太阳方位角 $\phi_S$ 定义。方位方向（N、S、E、W）与 xy 平面的关系由系统朝向的输入共同决定。

---

*sin θ 依赖源于将各向同性光照视为来自一个半球（类似天空）。因此，sin θ 反映了从正上方（θ = 0）到地平线（θ = π/2）之间，可见“天空面积”随 θ 增大而增多的事实。在高斯分布的情形下，我们将光照视为来自一个水平平面（类似电池测试仪的扩散板），因此不存在 sin θ 依赖。