光学层

本节介绍 SunSolve Power 中的光学层。

基板和薄膜

层有两种类型：基板和薄膜。

基板是厚的光学非相干层。光与基板的相互作用通过几何光线追迹和比尔定律计算。

薄膜是薄的光学相干层，与基板的形态保持一致。光与薄膜或薄膜堆栈的相互作用通过一维薄膜矩阵方法计算。

默认情况下，基板的厚度限制在 1–10⁵ μm 范围内，薄膜的厚度限制在 0.001–1 μm 范围内。如果你希望修改这些限制，请写信至 support@pvlighthouse.com.au。

基板

可以在层标签页上向组件添加或移除基板。每个基板具有

1. 一种材料，其复折射率可在折射率库中找到；以及
2. 一个体厚度。

两个基板之间的界面由以下定义：

• 一个织构形态，其中织构的高度不包括在体厚度中；
• 一个光学散射模型；
• 以及以下任一项
  • 一个薄膜堆栈，其中每个薄膜都有自己的材料和厚度；或
  • 一个具有定义的反射率、吸收率和透射率的”反射器”。

下图显示了基板的总厚度如何取决于用户输入的体厚度和表面织构高度。

薄膜

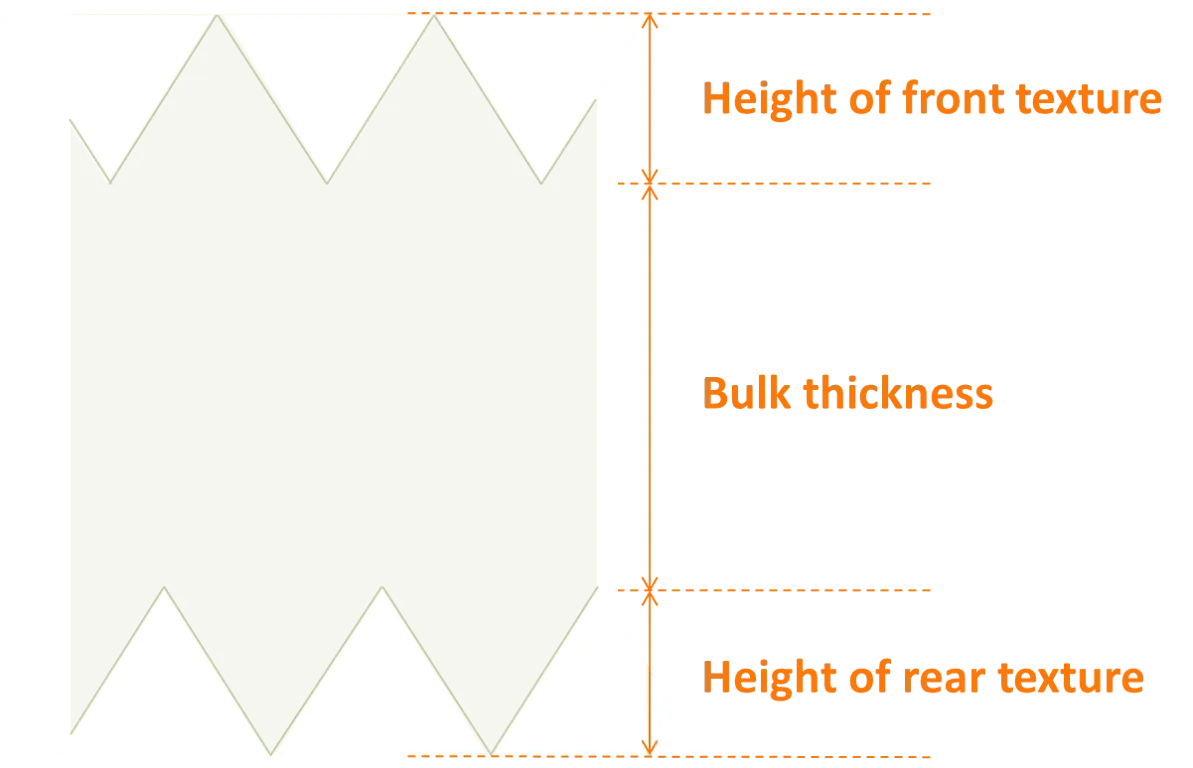
可以在基板之间的任何界面处添加或移除薄膜，其中每个薄膜具有

1. 一种材料，其复折射率可在折射率库中找到；以及
2. 一个厚度。

薄膜的厚度用于计算界面的光学行为，以及如果需要，计算薄膜内的产生剖面。然而，薄膜的厚度不会对组件的厚度有贡献，组件的厚度仅由基板的厚度及其形态计算得出。

薄膜厚度表示下图所示的尺寸。它定义了垂直于底层平面方向上的薄膜厚度。因此，假定薄膜与织构完全保形。

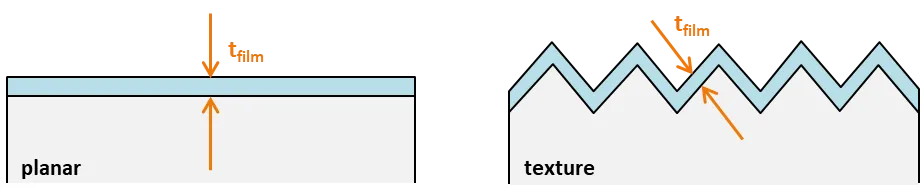
薄膜厚度可以是恒定的或可变的。如果是可变的，则每次光线与界面相互作用时都会重新计算薄膜厚度。在这种情况下，可以应用两种概率函数之一：(a) 顶帽函数或 (b) 高斯函数。这些函数的示例在下面左图中绘制。如果选择高斯分布，则对厚度应用上限和下限；限制不能大于平均值的 4 个标准偏差，下限不能小于零。

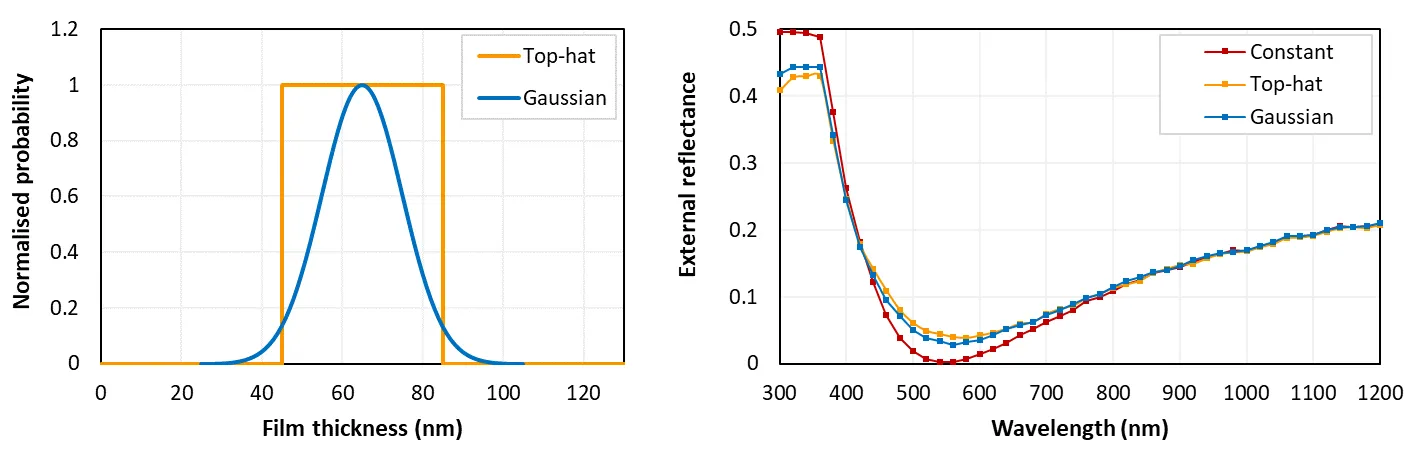
上图给出了薄膜厚度的不同选项如何影响结果的示例。右图绘制了平面硅涂有三种厚度的 SiNₓ 薄膜的外部反射：(i) 恒定 65 nm，(ii) 65 ± 20 nm 的顶帽函数，以及 (iii) 平均值为 65 nm、标准偏差为 10 nm、下限和上限分别为 25 和 105 nm 的高斯函数。这些函数在左图中绘制。

默认情况下，SunSolve 假定所有薄膜具有恒定厚度。要设置具有可变厚度薄膜的界面，请导航到选项标签页，选中”启用可变 $t_{\text{film}}$“并选择所需的界面。然后，所选界面将包含定义可变厚度薄膜所需的附加输入。

材料属性

SunSolve 计算光线穿过材料时以及与材料之间的界面相互作用时的光学行为。这些计算需要了解每种材料的波长依赖复折射率：$n(\lambda)$ 和 $k(\lambda)$。

材料可以从我们的预加载数据集中选择，也可以从你自己的数据集中选择。有一个视频解释了如何上传数据集，所有 $n(\lambda)$ 和 $k(\lambda)$ 数据都可以在我们的折射率库中绘制和下载。

要确定某个所需波长 $\lambda'$ 处的 $n$ 和 $k$，SunSolve 对折射率数据集进行线性插值。如果 $\lambda'$ 短于数据集中可用的最短波长，SunSolve 假定 $n(\lambda')$ 和 $k(\lambda')$ 等于最短可用波长处的 $n$ 和 $k$。对长波长应用等效假设。下图说明了这种方法。

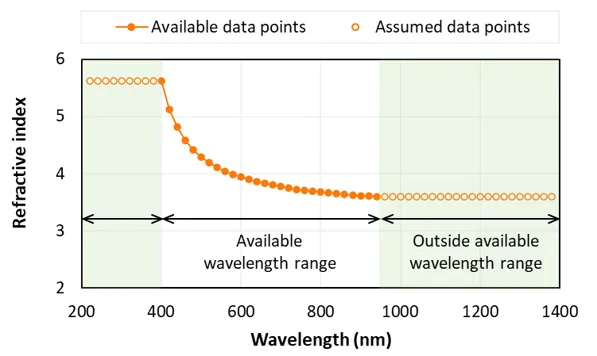
收集层和光生电流

“收集”层对组件产生的电流有贡献。也就是说，收集层吸收的光子的某个部分被转换为自由载流子并被”收集”，从而对太阳能电池的光生电流有贡献。

在大多数 SunSolve 模板中，主基板是唯一的收集层。与具有 c-Si 太阳能电池的常规组件一样，只有硅基板产生电流。

然而，可以将其他层设置为收集层。例如，太阳能电池正面的薄膜可以是收集层，如异质结太阳能电池中的 a-Si 薄膜，或钙钛矿–硅串联太阳能电池的钙钛矿层。

尽管任何薄膜都可以是收集层，但 SunSolve 只允许一个收集基板，从而防止了 GaAs–Si 串联太阳能电池的仿真。我们计划在未来的升级中发布多个收集基板的选项。

所有收集层都对相同的光生电流 $J_L$ 有贡献：

$$J_L = \sum\limits_{i}{J_{Li}},$$

其中 $i$ 表示每个收集层，并且

$$J_{Li} = \int_{0}^{\infty}{J_{\text{ph}}(\lambda)A_{i}(\lambda)\eta_i(\lambda)d\lambda},$$

其中 $J_{\text{ph}}(\lambda)$ 是由光照标签页上的输入确定的入射光子电流，$A_i(\lambda)$ 是通过光线追迹确定的被收集层内的带间过程吸收的入射光的分数，$\eta_i(\lambda)$ 是收集层的收集效率。

这个计算得到的 $J_L$ 值由电学求解器用于计算仿真的电池或组件产生的电流–电压曲线和最大功率。

可以在电路标签页的”收集效率”部分将层分配为”收集”层。一旦将层分配为收集层，其收集效率可以设置为恒定或随波长变化。

层吸收

半导体中有两种类型的光学吸收：带间吸收 (BBA) 和自由载流子吸收 (FCA)。

当光被 BBA 过程吸收时，意味着价带内的电子接收到足够的能量被转移到导带。新激发的电子成为”自由载流子”，它对光生电流有贡献。（这也意味着空穴从导带转移到价带，它也成为自由载流子。）

当光被 FCA 过程吸收时，光子的能量被已经在导带中的电子或已经在价带中的空穴吸收。尽管此过程将自由载流子转移到更高的能态，但它很快失去该能量（作为热量），载流子返回到其原始状态。与 BBA 不同，FCA 不对光生电流有贡献。

在 SunSolve 中，可以计算两种吸收源。

默认情况下，SunSolve 假定收集材料的折射率的虚部表示 BBA。在这种情况下，所有这种吸收都对产生电流有贡献。（虚部 $k$，通常称为消光系数，通过方程 $\alpha = 4\pi k/\lambda$ 与吸收系数 $\alpha$ 相关。）

然而，可以同时计算 FCA 和 BBA。为此，请在选项标签页上选中”包括 FCA”，并在 FCA 面板中选择哪些收集层具有 FCA。

对于分配了 FCA 的每一层，用户必须首先定义其材料数据集中 $k$ 值的含义。请记住，材料是在层标签页上选择的，它们的折射率数据集，即 $n(\lambda)$ 和 $k(\lambda)$，可以从我们的折射率库下载。

具体来说，FCA 表中”Optn”下的复选框为用户提供了将材料的 $k$ 定义为包括或排除 FCA 的选项。未选中时，$k = k_{\text{BBA}}$，选中时，$k = k_{\text{BBA}} + k_{\text{FCA}}$。例如，Si 中 $k$ 的已发布数据几乎总是排除 FCA，在这种情况下 $k = k_{\text{BBA}}$，输入应该未选中。在其他材料中，$k$ 可能来自材料总吸收的测量，在这种情况下 $k$ 将包括 BBA 和 FCA，输入应该选中。

接下来，用户为每一层分配一个 FCA 模型。有两种类型的模型：

1. 已发布的模型，用户输入自由电子和自由空穴的浓度，SunSolve 通过我们的FCA 计算器中描述的方程计算 $k_{\text{FCA}}$。这些 FCA 模型在下面的下一节中更详细地描述。
2. 自定义模型，其中 $k_{\text{FCA}}$ 等于用户选择的材料中的 $k$。应用此选项时，用户通常会选择一个自定义材料，其值专门设置为所需的 $k_{\text{FCA}}$。

通过这些输入，用户已将某些层分配为具有两个消光系数：$k_{\text{BBA}}$ 和 $k_{\text{FCA}}$，其中组合消光系数简单地为 $k_{\text{Tot}} = k_{\text{BBA}} + k_{\text{FCA}}$。

然后 SunSolve 使用所有层的 $k_{\text{Tot}}$ 求解光线追迹，以确定每一层中的总吸收率 $A_{\text{Tot}}$。在光线追迹之后，归因于 BBA 和 FCA 的吸收分数分别为 $A_{\text{BBA}} = k_{\text{BBA}}/k_{\text{Tot}}$ 和 $A_{\text{FCA}} = k_{\text{FCA}}/k_{\text{Tot}}$。（我们尚未找到此假设的引用。）

我们感谢 Hanwha Q cells 共同资助了包括自由载流子吸收的升级。

自由载流子吸收模型

晶体硅中的 FCA

SunSolve 提供了几个模型来根据自由载流子浓度计算 c-Si 的 FCA，其中大多数假设温度为 300 K。

1. 经典德鲁德模型：Smith (1959)、Schroder (1978)（方程 1）和 Isenberg (2004)（方程 1，其中第二个因子为单位）中的方程。
2. Schroder (1978)：Schroder (1978) 中的方程 5 和 6。拟合 λ > 4000 nm 和 c-Si 中 10¹⁶ 至 10¹⁹ cm⁻³ 的掺杂浓度的数据。
3. Green (1995)：Green (1995) 中的方程 4.8。推导出 λ > 2500 nm 和 c-Si 中 ~10¹⁸ cm⁻³ 的载流子密度。
4. Isenberg (2004)：Isenberg (2004) 中的方程 4 及表 I 中的参数。限制在 c-Si 中的 1200 nm。
5. Rudiger (2013)：Rudiger (2013)。从扩散 c-Si 中 1200 nm < λ < 2000 nm 范围内的实验数据拟合得出，载流子浓度在 10¹⁷ 和 10²⁰ cm⁻³ 之间。
6. Xu (2013)：Xu (2013)。从扩散 c-Si 中 1000 nm < λ < 1200 nm 范围内的实验数据拟合得出，载流子浓度在 10¹⁷ 和 10²⁰ cm⁻³ 之间。
7. Baker-Finch (2014)：Baker-Finch (2014)。从扩散 c-Si 中 1000 nm < λ < 1500 nm 范围内的实验数据拟合得出，掺杂浓度在 10¹⁸ 和 3 × 10²⁰ cm⁻³ 之间。
8. Baker-Finch LL (2014)：Baker-Finch (2014)。最佳拟合参数化的下限。
9. Baker-Finch UL (2014)：Baker-Finch (2014)。最佳拟合参数化的上限。

第一个 FCA 模型源自固体中自由载流子随机碰撞的经典”德鲁德”处理。通常应用 Smith (1959) 的方法（例如，在 Schroder (1978)、Horwitz (1980)、Isenberg (2004)、Rudiger (2013) 中），在此实施例中，$k_{\text{FCA}}$ 与自由载流子浓度呈线性关系，与波长呈抛物线关系。用户还必须输入自由载流子的迁移率。我们应用 Schroder (1978) 的方程 1。其余模型是 300 K 下 c-Si 的参数化。

任何材料中的 FCA

SunSolve 还包括一个”通用参数化”模型：

$$\alpha_{\text{FC}} = K_n \cdot n \cdot \lambda^a + K_p \cdot p \cdot \lambda^b,$$

其中 $K_n$、$K_p$、$a$ 和 $b$ 是常数，$n$ 和 $p$ 是以 cm⁻³ 为单位的电子和空穴浓度，$\lambda$ 以 nm 为单位。此方程是除德鲁德和 Isenberg 模型之外的所有上述模型的一般形式。

PC1D 也使用通用参数化。PC1D 帮助文件包含来自旧来源（1967、1978、1981）的 c-Si 和一些 n 型半导体的输入；通过在 PC1D 帮助中导航”device menu”→“region parameters”→“material”找到它们。

FCA 建议

对于 300 K 下的晶体硅（包括多晶硅），建议使用 Baker-Finch 模型 (2014)。对于其他材料和温度，建议使用从实验测量得出的自定义 FCA 数据，或者如果有代表性的输入可用，则使用通用参数化。