光学散射

散射模型

光学散射可以通过三种模型之一来实现：‘no scattering’（无散射）、‘Lambertian scattering’（朗伯散射）或 ‘Phong scattering’（Phong 散射）。下图给出了这些模型的示意。

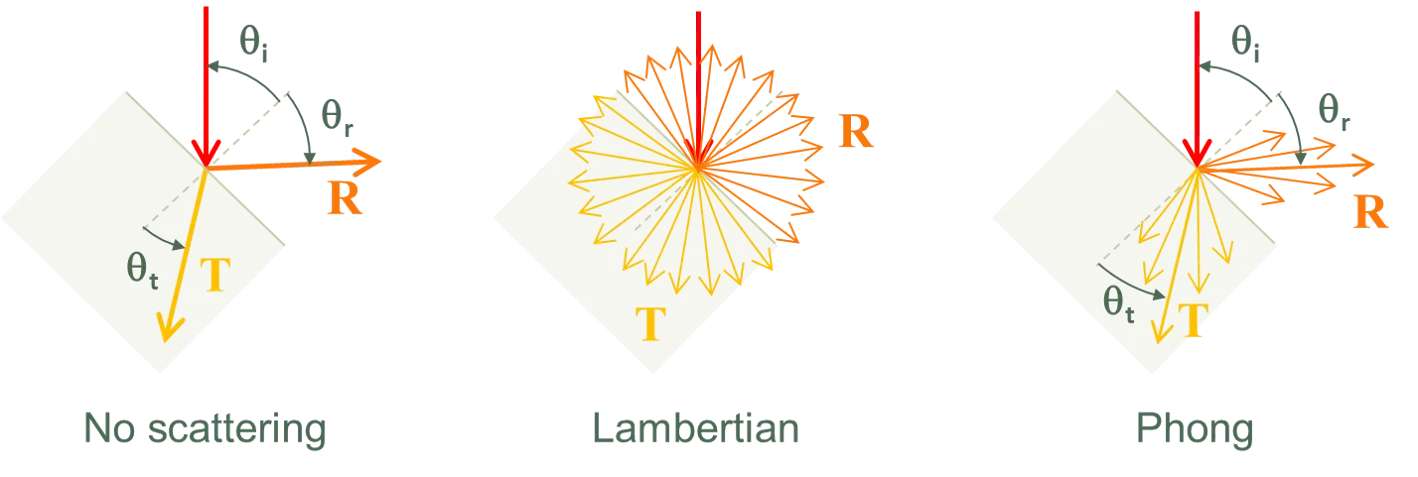
每当光线与某个界面相交时，SunSolve 首先根据 General 标签页中描述的随机方法判定该光线是被反射还是透射，然后再根据所选散射模型确定光线的新传播方向。

在 no scattering 模式下，假定界面为理想镜面，反射角 $\theta_r$ 等于入射角 $\theta_i$，透射角 $\theta_t$ 由斯涅尔定律给出。

在 Lambertian scattering 模式下，决定光线新方向的球坐标角（θ 和 φ）按下式随机生成：

$$\theta = \arccos \left( {\chi^{\frac{1}{2}}} \right),$$

and

$$\phi = 2\pi\chi,$$

其中 χ 是一个随机数，0 ≤ χ < 1，并且用于 θ 和 φ 的随机数互不相同。

当光线数量足够多时，这些方程会产生朗伯反射（或透射），即每单位立体角的光强均匀。注意，新光线方向与入射角 $\theta_i$ 无关。

在 Phong scattering 模式下，SunSolve 将新方向确定为

$$\Delta\theta = \arccos\left ({\chi^{\frac{1}{\alpha + 1}}}\right )$$

and

$$\phi = 2\pi\chi,$$

其中 α 称为 Phong 指数，Δθ 表示新角度与镜面反射（或镜面透射）之间的差值：对于反射，Δθ = θ – $\theta_r$；对于透射，Δθ = θ – $\theta_t$。这一实现遵循 Schümacher 提出的用于随机光线追迹的 Phong 模型。

因此，当 α = 1 且 $\theta_i$ = 0（法向入射）时，Phong 散射等价于朗伯散射；当 α → ∞ 时则等价于“无散射”。在实际使用中，α = 1,000,000 已足够逼近镜面表面。SunSolve 将 α 限制在 1 ≤ α ≤ 1,000,000 范围内。

下图展示了概率函数 $f(\Delta\theta) = (\cos\Delta\theta)^{1+\alpha}$ 随 Δθ 和 α 的变化情况（注意：这不是强度函数）。

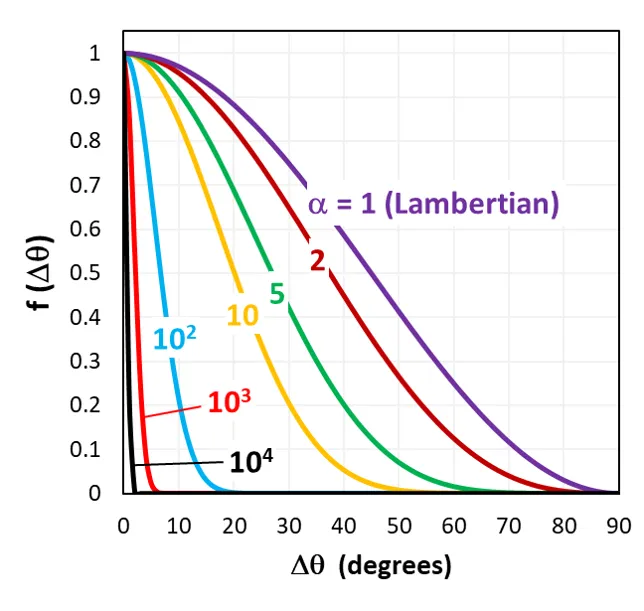
从上图可以看出，Phong 散射可以用来模拟“聚焦”散射。例如，当 α = 1000 时，反射光大致集中在 θ = $\theta_r$ ± 5° 范围内。这在模拟基角在 ± 5° 范围内随机变化的金字塔纹理时尤为有用。

散射分数

计算入射光线中被散射部分的比例 Λ 有两种方法。

第一种方法是设定一个恒定的散射分数 Λ。也就是说，每当光线与表面相互作用时，其中有 Λ 的比例按所选散射模型处理，其余部分不发生散射。因此，当 Λ = 0 时，无论选择哪种散射模型，界面都等价于“无散射”。

第二种方法是应用标量散射模型（scalar scattering model）。在该模型中，散射分数 Λ 不再是常数，而是随波长增加而减小，并且还依赖入射角、材料折射率以及光线是被反射还是被透射。

For reflection,

$$\Lambda = 1 - \exp\left [- ( \frac{2\pi}{\lambda} \cdot \sigma_{\text{rms}} \cdot 2 \cdot n_i \cdot \cos\theta_i) ^ 2 \right],$$

and for transmission,

$$\Lambda = 1 - \exp\left [- ( \frac{2\pi}{\lambda} \cdot \sigma_{\text{rms}} \cdot \left| n_i \cdot \cos\theta_i - n_t \cdot \cos\theta_t \right | ) ^ 2 \right],$$

其中 $\sigma_{\text{rms}}$ 是表面均方根粗糙度。

下图给出了在入射介质折射率 $n_i = 1.5$ 时，根据标量散射模型计算得到的散射分数随波长和 $\sigma_{\text{rms}}$ 的变化情况。图中分别绘制了入射角 $\theta_i = 0°$（实线）和 50°（虚线）的结果。

补充说明

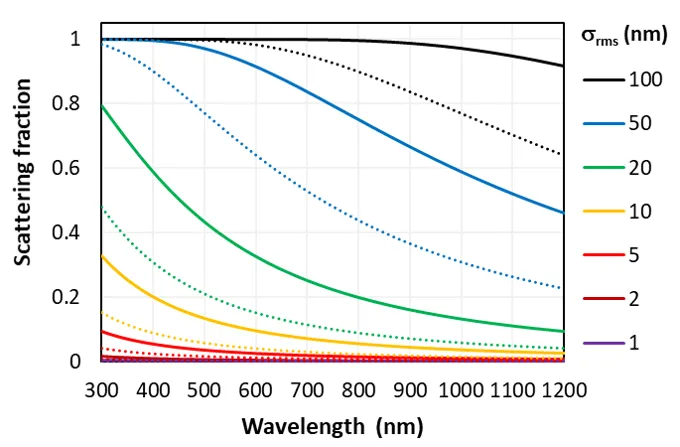
这里再补充三点说明。

首先，当在某个界面上施加 Lambertian 或 Phong 散射时，SunSolve 会在光线与该界面相互作用后随机化其偏振状态。在这种情况下，Phong 模型得到的结果可能会与“无散射但跟踪偏振”的情况略有不同。

其次，在 Phong 散射与非法向入射（$\theta_i > 0$）同时存在时，计算得到的新方向有可能出现 θ > 90° 的情况。如果允许这种情况，就会出现本应被反射的光线被当作透射处理，或本应被透射的光线被当作反射处理的情况。为避免这种物理上的不合理性，SunSolve 在 Phong 模型中不允许 θ > 90°：一旦计算得到 θ > 90°，就将其重新设定为 θ – 90°。

最后，我们说明一下用于随机光线追迹的 Phong 模型实现方式，它遵循 Schümacher 等人的处理方法（部分论文并未显式给出所用方程，但作者已向 PVL 方面确认了其做法）。

Phong 提出的经典散射公式最初是为图形渲染而设计的，而非用于随机光线追迹。因此，在将其用于光线追迹时存在一定的实现歧义，我们欢迎就此进行反馈和讨论。

我们将 Phong 的定义改述如下：从表面反射到观察者方向的相对光强为 $R$ [cos β]^α，其中 $R$ 为表面反射率，β 为观察方向与若为镜面反射时反射方向之间的夹角（即前文所称 Δθ）。此外，假定光源和观察者都位于距表面无限远处。

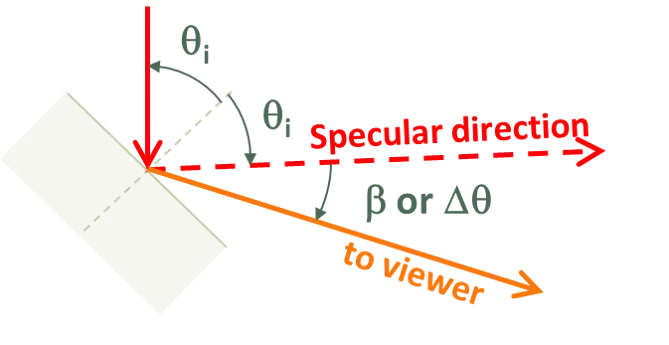
因此，在考虑朗伯余弦定律（即照明强度随 cos β 衰减）之后，在角度 β 方向上由表面反射的光子分数可写为 $R$ [cos β]^{α + 1}。

如何在光线追迹中应用这一函数并不十分明确。从理想光线追迹的角度看，恰好在 β 角度上不会有光线被反射，因此该角度处的强度应为零。相反，我们需要定义落在某一立体角范围内的光线分数，例如无穷小立体角 $d\Omega = \sin\theta d\theta d\phi$，并由此推导光线在 0 到 β 之间传播的概率，从而得到概率函数 $f(β)$。

当这一方法应用于各向同性照明（例如朗伯反射）且每个 $d\Omega$ 内的反射强度为常数时，可以推导出如下概率函数：

$$f(\beta) = -2\int_{0}^{\beta}\cos{\theta}\sin{\theta}d\theta = \left(\cos\theta \right)^2.$$

因此，如果将 Phong 给出的强度理解为 $d\Omega$ 内的强度，则相应的概率函数应为

$$f(\beta) = -2\int_{0}^{\beta}\left(\cos{\theta}\right)^{\alpha}\sin{\theta}d\theta.$$

如果反过来，将 $R$ [cos β]^α 理解为在 0 到 β 之间的强度分布，则概率分布可以采用更简单的形式：

$$f(\beta) = \left(\cos\beta \right)^{\alpha+1}.$$

第一种处理方式在概念上更契合 Phong 的原始定义，但第二种形式更为简洁，也已有先例被采用。在这两种情形下，朗伯散射都对应某一特定的 α 值（例如 α = 1），这一点很“优雅”但并非硬性要求。（也有研究可能采用了 f(θ) = [cos β)]^α 形式，此时朗伯散射对应 α = 2。）

总之，SunSolve 采用了 Schümacher 提出的 Phong 模型实现方式，同时也欢迎就其他可能的实现方案进行讨论。