日照

在每个时间步长，SunSolve计算

• 太阳位置，即太阳天顶角和方位角；
• 直射光和漫射光的太阳光谱；以及
• 归因于光束和各向同性组件的阳光分数。

本节描述用于这些计算的模型。下表总结了SunSolve Yield中用于计算日照的默认模型。

参数	模型	参考文献
AM0光谱	IEC标准	[IEC2008]
晴空光谱	SPECTRL2	[Bird1986]
阴天光谱	Ernst	[Ernst2016]
太阳位置	Reda and Andreas	[Reda2004]
大气质量	Karsten	[Karsten1989]
漫射光天空分布	Perez 1990	[Perez1990]
地球-太阳修正因子		[Bird1986]
时间方程		[Reno2012]

太阳位置

一般定义

• 太阳天顶角和太阳方位角是相对于太阳中心定义的。

• 太阳天顶角定义为当太阳正在头顶时为0°。

• 太阳方位角定义为从北方顺时针方向，即，北方 = 0°，东方 = 90°，南方 = 180°，西方 = 270°。

• 日出和日落定义为天顶角为90°时的时间（精确到秒）。

设置太阳位置的选项

用户可以

1. 将太阳位置设置为气象文件中的值，或

2. 允许SunSolve根据系统位置、日期和时间计算太阳位置。

对于第一个选项，用户加载一个在每个时间步长包含太阳位置的气象文件。该位置可以用太阳天顶角或太阳高度角（即，在地平线时为0°，正在头顶时为90°）来定义，太阳方位角定义为从北方顺时针方向或在不同气象服务中找到的其他各种定义。¹

无论输入如何，SunSolve的太阳位置输出始终是太阳天顶角和方位角，如上述”一般定义”中所定义。

对于第二个选项，用户选择太阳矢量（不受大气影响）和大气折射的算法。

太阳矢量模型

有七个太阳矢量模型。参考文献包含相关方程：

1. Reda and Andreas 2004 [Reda2004]。

2. Blanco–Murial 2001 [Blanco2001]。

3. Michalsky 1988 [Michalsky1988]。

4. Walraven 1979 [Walraven1978]。

5. Spencer 1971，我们的实现来自[Reno2012]

6. ASCE (2012)，我们的实现来自[Reno2012]

7. PVSyst，如PVSyst文档中所述（截至2023年4月）。

最复杂的太阳矢量模型是Reda and Andreas 2004模型。它实现了Meeus在1998年开发的算法，用于计算公元前2000年至公元6000年之间的天顶角和方位角，精度在±0.0003°以内。SunSolve中的实现经过修改，排除了折射，以便可以单独计算其影响。自2023年5月以来，此模型一直是SunSolve中的默认模型。

第二复杂的模型是Blanco–Muriel 2001，它在1999年至2015年之间计算太阳矢量的精度在0.5弧分以内。这是SunSolve在2023年5月之前的默认模型。

其他模型更简单且不太准确，它们包含在SunSolve中以允许与历史太阳矢量算法和其他软件进行比较。

大气折射模型

SunSolve有三个大气折射选项：

1. 无，即不应用由于折射引起的太阳位置修正。

2. Reda and Andreas (2004) [Reda2004]。

3. Zimmerman (1981) [Zimmerman1981]。

Reda and Andreas模型是最准确的。它需要海拔、气压和环境温度的输入。这些输入可以与气象数据一起加载，但如果没有，则假设为0 m、1013.3 mbar和25°C。²

时间间隔的太阳位置

SunSolve计算一系列时间间隔的产量，并将它们相加以确定总产量。这在上一节中有所描述。

对于大多数时间间隔，太阳位置在该间隔的中点计算。例如，如果SunSolve正在计算上午10-11点的产量，它会在上午10:30计算太阳位置。

包含日出或日落的任何间隔会出现例外情况。在这种情况下，太阳位置在日光期间的中点计算。³ 例如，当日出在上午6:30时，上午6-7点间隔的太阳位置将在上午6:45计算。当日落在下午5:40时，下午5-6点间隔的太阳位置将在下午5:20计算。

太阳光谱

在每个时间步长计算直射和漫射光谱，如下所示：

1. 计算大气外光谱。

2. 计算晴空条件下的直射和漫射光谱。

3. 针对云层修改直射和漫射光谱。

4. 缩放直射和漫射光谱的光谱强度，使积分辐照度等于所需的DNI和DHI。

5. 将光谱辐照度转换为光子通量。

我们以280-4000 nm的波长范围和5 nm的间隔（744个波长区间）确定步骤1-4。此范围涵盖太阳光谱强度的99%以上。在步骤5中，范围减少到300-1200 nm，间隔增加到20 nm（46个区间）。此范围仅涵盖硅半导体的有源区域。对所有46个波长区间进行光线追踪。

大气外光谱，AM0

大气外光谱定义了到达地球外层大气的太阳光谱。SunSolve使用IEC标准[IEC2008]中的AM0光谱，该标准定义了地球距太阳平均距离时的光谱。

然后，SunSolve在每个时间间隔将光谱强度乘以”地球-太阳因子”。该因子由[Bird1986]中的方程3和4确定，并考虑了地球轨道的椭圆性质。（它在4月3日和10月1日左右为1。）

晴空光谱

SPCTRAL2算法[Bird1986]用于确定晴天直射光和漫射光通过地球大气的波长相关透射率，然后用于将AM0光谱转换为直射和漫射光谱。

除了时间和全球位置外，该算法还需要六个输入：大气质量、远场反照率以及定义大气的四个参数：气压、500 nm处的浊度、可降水水汽浓度和臭氧浓度。

六个输入中最有影响的是大气质量AM，从太阳天顶角θs计算，

$$AM = \begin{cases} \frac{1}{\cos \theta_s + 0.50572 \times (96.07995 - \theta_s)^{-1.6364}}, & \theta_s \leq 91.8° \\ 64.8, & \theta_s > 91.8° \end{cases}$$

对于θs ≤ 91.8°，该方程是Karsten和Young [Kasten1989]的广泛使用的参数化。在SunSolve中，我们将计算限制在θs < 91.8°以防止崩溃。⁴

其余五个输入与气象数据一起加载，或者如果它们不可用，则应用默认值。下表列出了这些输入、默认值⁵和用于确定特定位置输入的可能来源。默认值是当大气质量为1.5时用于生成AM1.5g光谱的值。请注意，反照率仅对漫射光的光谱强度有贡献，因为光可以从地面反射到天空，然后再次反射到地面；在SPCTRAL2中假设它与波长无关。⁶

模拟中使用的大气输入，按它们对太阳光谱的影响程度排序。NASA数据可以从Giovani网站获取

属性	单位	AM1.5g默认值	SunSolve7	可能来源
可降水水汽	cm	1.416	在气象中加载	TMY气象文件（Meteonorm、SolarGIS）
500 nm处的浊度		0.084	在气象中加载	NASA：时间序列，区域平均气溶胶光学深度500 nm每日1度。
臭氧	DU	343.8	在气象中加载	NASA：时间序列，区域平均臭氧总柱（类似TOMS）每日1度。
大气压	mbar	1013.25	在气象中加载	TMY气象文件（Meteonorm、SolarGIS）
远场反照率		10%	在气象中加载	现场测量、TMY气象文件、卫星数据。

请参阅大气对光谱的影响以了解这些因素如何影响直射光谱的图表。

阴天光谱

为了考虑云层，以类似于[Ernst2016]描述的方式调整晴空光谱。⁸ 在每个时间步长，程序如下：

1. 使用SPECTRL2在280 ≤ λ ≤ 4000 nm范围内以5 nm步长确定晴空条件下的直射（光束）$I_{B\text{ clear}}(\lambda)$、漫射$I_{D\text{ clear}}(\lambda)$和总$I_{G\text{ clear}}(\lambda)$辐照度。

2. 阴天条件下的直射（光束）光谱等于缩放的晴空直射光谱以给出测量的DNI，

   $$I_{B \text{ cloudy}}(\lambda) = I_{B \text{ clear}}(\lambda) \cdot \frac{DNI}{\int_{280}^{4000 \text{ nm}} I_{B \text{ clear}}(\lambda) d\lambda}$$

   即，无论晴天还是阴天，直射光的相对光谱都是相同的。

3. 计算云不透明度因子OF。它与从气象文件中获取的直射法向日照DNI除以晴空光谱的DNI（即步骤1的$I_{B\text{ clear}}(\lambda)$）有关：

   $$OF = 1 - \frac{DNI}{DNI_{\text{clear}}} = 1 - \frac{DNI}{\int_{280}^{4000 \text{ nm}} I_{B \text{ clear}}(\lambda) d\lambda}$$

   因此，OF量化了不穿透云层的直射光的分数。 请注意，如果$DNI > DNI_{\text{clear}}$，我们覆盖此方程并设置OF = 0。

4. 阴天条件下的未缩放漫射光谱由以下给出

   $$S_{D \text{ cloudy}}(\lambda) = I_{D \text{ clear}}(\lambda) + OF \cdot I_{B \text{ clear}}(\lambda) \cdot \cos(\theta_z),$$

   即，晴空漫射光谱加上不穿透云层的晴空直射光谱。

5. 然后缩放阴天条件下的漫射光谱以给出气象文件的DHI

   $$I_{D \text{ cloudy}}(\lambda) = S_{D \text{ cloudy}}(\lambda) \cdot \frac{DHI}{\int_{280}^{4000 \text{ nm}} S_{D \text{ cloudy}}(\lambda) d\lambda}.$$

通过采用这种方法，我们假设（i）阴天的直射光谱与晴天相同，只是衰减了，（ii）漫射光谱与晴天相同，只是衰减并与总光谱结合。

实际上，这种方法将云层视为中性密度滤光片和中性密度散射器。

实际上，通过云层的透射率往往随波长而降低。PV Lighthouse正在允许SunSolve用户选择考虑这一点的阴天光谱模型。NREL的FARMS-NIT程序提供了一个阴天光谱模型，但它目前不区分直射和漫射阴天光谱（2025年3月）。

漫射光的天空分布

SunSolve Yield为漫射光的天空分布提供三个选项：（1）各向同性，（2）Hay-Davies模型，以及（3）Perez模型。在第一种情况下，光的角度分布基于天气条件不变，并且始终假设从天空中所有点均匀。在Hay-Davies和Perez模型中，云量用于将部分漫射辐照度分配到太阳位置周围的环日区域。更多云层导致更多各向同性条件，晴朗日导致更多环日成分。环日光的角度假设等于太阳天顶角（即，它似乎直接来自太阳）。在Perez模型的情况下，已经实现了几个变体。

Hay-Davies模型

在每个时间步长使用以下程序应用Hay-Davies模型：

1. 使用以下方程计算天空晴朗度指数（$K_b$）：

   $$K_b = \frac{I_{\text{direct,perp}}}{I_0 \times d}$$

   其中$I_{\text{direct,perp}}$是DNI的强度，$I_0$是阳光的大气外强度1367 W/m2，d是使用[Bird1986]的方程2计算的地球-太阳修正因子：

   $$d = 1.00011 + 0.034221 \times \cos \psi + 0.00128 \times \sin \psi + 0.000719 \times \cos 2\psi + 0.000077 \times \sin 2\psi$$

   ψ是使用[Bird1986]从以下计算的以弧度表示的天数：

   $$\psi = 2\pi \times \frac{(\text{DayOfYear} - 1)}{\text{DaysInYear}}$$

2. 然后使用Kb的值调整直射光和漫射光的强度，如下所示：

   $$J_{\text{ph,direct normal}}(\lambda) = J_{\text{ph,direct normal}}(\lambda) + \frac{K_b \times J_{\text{ph,diffuse horizontal}}(\lambda)}{\cos \theta_s}$$ $$J_{\text{ph,diffuse horizontal}}(\lambda) = (1 - K_b) \times J_{\text{ph,diffuse horizontal}}(\lambda)$$ $$DNI = DNI + \frac{K_b \times DHI}{\cos \theta_s}$$ $$DHI = DHI - K_b \times DHI$$

   其中$θ_S$是太阳天顶角。

Perez模型

SunSolve中包含Perez模型的三个实现。

• Perez (1987) - 基于[Perez1987]的Perez模型的早期版本。

• Perez (1990) - 基于[Perez1990]的Perez模型的较新版本。这是最常用的Perez模型。

• Perez (SAM) - NREL为在System Advisory Model工具中使用而改编的Perez 1990版本[Gilman2018]。

倾斜平面上漫射辐照度的Perez模型（[Perez1990]中的方程9，[Loutzenhiser2007]中的方程12）是

$$G_{SF\_dif} = DHI \cdot \left[(1 - F_1) \cdot \frac{1 + \cos \beta}{2} + F_1 \frac{a}{b} + F_2 \sin \beta\right], \tag{1}$$

其中$F_1$和$F_2$是环日和水平亮度系数，其中a和b由以下给出⁹

$$a = \max(0, \cos \theta_i) \tag{2}$$

和¹⁰

$$b = \max(0.087, \cos \theta_s), \tag{3}$$

亮度系数由以下给出¹¹

$$F_1 = f_{11} + f_{12}\Delta + f_{13}\theta_s \tag{4}$$

和

$$F_2 = f_{21} + f_{22}\Delta + f_{23}\theta_s \tag{5}$$

其中

$$\Delta = AM \cdot \frac{DHI}{DNI_0}, \tag{6}$$

其中AM是相对光学大气质量。¹²

f系数是从特定位置的经验数据的统计分析中得出的，它们取决于天空晴朗度ε，¹³

$$\varepsilon = \frac{\frac{DHI + DNI}{DHI} + 1.041 \cdot \theta_s^3}{1 + 1.041 \cdot \theta_s^3}, \tag{7}$$

因此，在没有直射光的阴天，DNI = 0，晴朗度ε = 1；在晴朗日，DNI增加，ε增加到1以上。

在[Perez1987]和[Perez1990]中已经推导出不同的f值，它们取决于ε的不同边界。表V和表VI给出了这些值。

表V： 晴朗度区间。

ε类别	上限
	[Perez1987]	[Perez1990]
1 – 阴天	1.056	1.065
2	1.253	1.230
3	1.586	1.500
4	2.134	1.950
5	3.230	2.800
6	5.980	4.500
7	10.080	6.200
8 – 晴天	–	–

表VI： f系数的值来自 (a) [Perez1987] 和 (b) [Perez1990]。这里我们使用辐照度系数而不是照度系数。

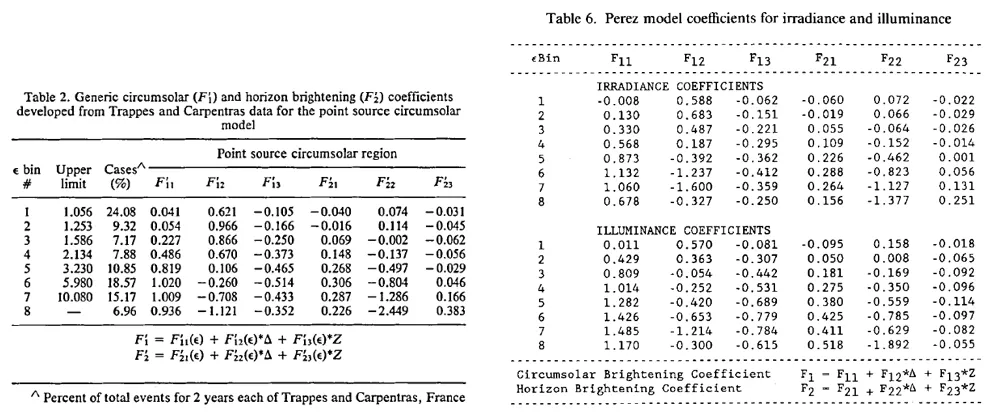
在每个时间步长使用以下程序应用Perez模型：

1. 使用方程（7）确定天空晴朗度（ε）。

2. 使用表VI（基于所选的Perez模型）计算Perez系数的值。应用线性插值来确定任何ε值的F值。请注意，SAM模型使用Perez1990系数。

3. 使用方程（6）确定天空亮度（Δ）

4. 使用方程（4）和（5）计算环日（F1）和地平线增亮（F2）的亮度系数。

5. 然后使用F1的值调整直射光和漫射光的强度，如下所示：

   $$J_{ph,direct\ normal}(\lambda) = J_{ph,direct\ normal}(\lambda) + \frac{F_1 \times J_{ph,diffuse\ horizontal}(\lambda)}{\max(0.087, \cos\theta_s)}$$ $$J_{ph,diffuse\ horizontal}(\lambda) = (1 - F_1) \times J_{ph,diffuse\ horizontal}(\lambda)$$ $$DNI = DNI + \frac{F_1 \times DHI}{\max(0.087, \cos\theta_s)}$$ $$DHI = DHI - F_1 \times DHI$$

   其中$θ_S$是太阳天顶角。

6. 假设地平线增亮从未与面板相互作用，因为模拟场是无限大的，该组件的入射角平行于平坦地面。因此，从场景中去除了一部分光。

Footnotes

1. SunSolve通过将加载的值与太阳位置的计算进行比较，自动尝试检测方位角定义，从中应用调整以将方位角映射到SunSolve定义上。 ↩

2. 太阳矩阵的计算（请参阅光学：太阳弧）假设这些默认值，而不考虑用户输入。该假设对SunSolve的结果影响可忽略不计，因为太阳矩阵使用正确的太阳位置（即，没有假设）进行插值。 ↩

3. 尽管这些时间间隔包含部分日光期间，但假设的GHI是完整期间的。因此，SunSolve在计算产量时将组件功率乘以完整期间。 ↩

4. 请注意，大于90°的太阳天顶角无论如何都被视为夜晚，不使用大气质量。 ↩

5. 这些默认值是NREL几十年前从科罗拉多州Golden的测量中开发的。不应期望它们适用于全球每个位置。 ↩

6. 请注意，此反照率值是”远场”反照率（定义为位置的气象文件的一部分），与在单位系统的光线追踪期间包含的波长相关反照率不同。 ↩

7. 如果用户未为特定位置定义，大气输入默认为AM1.5g值。 ↩

8. 虽然我们遵循Ernst et al的一般方法，但我们应用的实际方程有所不同。他们的方程7似乎有错误（省略了cosθz），方程5、7和8的组合在我们看来并不完全合乎逻辑，并且光学因子（方程5）是（ρ – ρclear）/（1 – ρclear），其中ρ = DHI/GHI，等效于OF = 1 –（DNI/GHI）/（DNIclear/GHIclear）而不是1 – DNI/DNIclear。然而，我们确实捕获了他们方法的目的（由Ernst传达）而不是确切的方程。也就是说，（i）无论晴天还是阴天，相对直射光谱都是相同的，（ii）相对漫射光谱是晴空漫射光谱加上未通过云层的任何晴空直射光谱，以及（iii）缩放光谱以确保其积分等于气象文件中的DNI和DHI。（不同于方程5、7和8的是第（ii）点。） ↩

9. 请注意，a/b = cosθi/cosθs，除了θi和θs限制为θi ≤ 90°和θs ≤ 85°。对a的限制确保当太阳在面板后面时环日为零。 ↩

10. 在[Loutzenhiser2007]中，他们使用b = max（85°，cosθs），这并不完全相同。 ↩

11. 在以下方程中，θs以弧度表示。Loutzenhiser2007强制F1 ≥ 0，但Perez1990似乎没有这样做。 ↩

12. Perez *et al.*引用Kasten1966的大气质量方程。SunSolve应用相同的方程。 ↩

13. 在Perez模型的第一篇论文[Perez1990]中，天空晴朗度是ε =（DHI + DNI）/ DHI。 ↩