基本光学

SunSolve光线追踪基于厚光学板（被视为光学非相干），这些板在相遇时具有复杂的光学界面。有两种类型的光学界面：（1）菲涅耳和（2）基本反射器。

在第一种类型（菲涅耳）中，反射、吸收或透射的百分比机会根据界面两侧材料的光学特性以及界面处的任何薄膜从基本物理确定。光学求解基于菲涅耳方程，使用传输矩阵方法的改编版本，并考虑光的偏振。在第二种情况（基本反射器）中，这些百分比被设置为程序的输入。它们通常基于实验测量确定。

光学界面还可以包括形态（通常称为纹理）和额外的散射。

下表提供了应用于界面的光学模型的摘要。

参数	模型	注释	参考文献
材料中的吸收	Lambert-Beer定律		-
界面处的反射、吸收、透射	菲涅耳	应用于菲涅耳界面	-
光线方向	斯涅尔定律
散射分数	固定	用户定义%	-
散射分数	标量散射模型		[Carniglia1979] [Dominé2010]
散射分布	朗伯散射
散射分布	Phong	修改以考虑透射	[Phong1975] [Schümacher1994]

有关SunSolve引擎所基于的物理的更详细解释，请读者参考Pietro Altermatt的在线讲座系列。

可在此处获得：https://pvlighthouse.com.au/cms/lectures/altermatt/optics/

菲涅耳界面

使用基本光学方程求解光学菲涅耳界面。这使用两侧材料板的波长相关折射率，结合任何存在的薄膜。这种求解用于确定光线被反射、透射或在界面处吸收的百分比机会。

基本反射器

定义为反射器的光学界面不应用任何复杂的光学界面求解。相反，它应用查找表，该表定义反射、吸收或透射的入射光的分数。该表可以定义为波长相关的。

组件表面对基本反射器的应用有额外的选项。这些包括反射、吸收和透射的角度依赖性。有关这方面的更多详细信息，请参见第6.1节。

纹理模型

界面的表面形态（即纹理）可以设置为几个选项之一。非平面选项的图像如下所示，其中图像描绘了在整个界面上在x和y方向上重复的特征。用户设置角度ω和表面特征的高度h或宽度。

请注意，（i）V槽延伸整个界面的x或y范围，具体取决于用户选择x或y方向；（ii）角立方体[Van2015]具有固定的ω和规则的六边形单位晶胞。

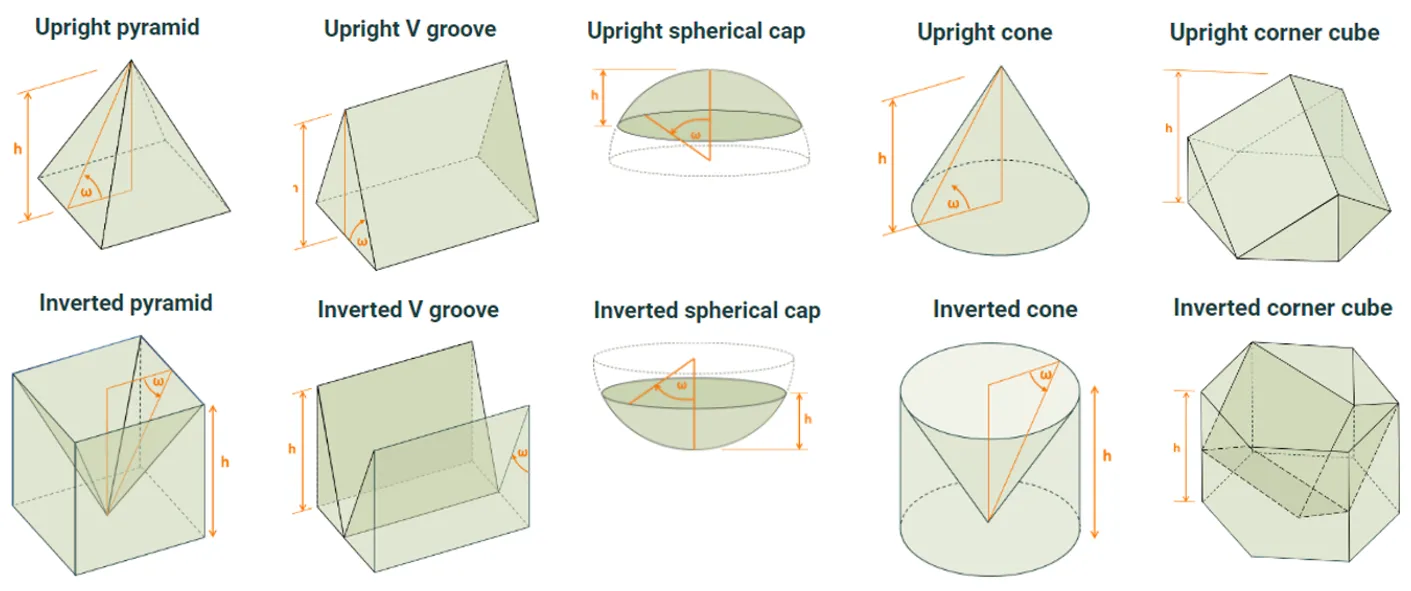非平面表面形态选项，显示为单位块。

随机形态

程序提供选择”随机”或”规则”表面形态（即纹理）的选项。这有助于模拟，例如，覆盖工业单晶硅晶片前表面的”随机”定向金字塔，或在高效率实验室PERL太阳能电池中采用的”规则”倒金字塔。

下图演示了”随机”形态如何影响光线追踪期间光线的传播。形态的最简单几何特征（例如，金字塔或沟槽）由其单位晶胞的平面界定。与单位晶胞壁相交的光线传播到相邻单位晶胞，而与单位晶胞底部（或顶部）相交的光线传播到特征下方（或上方）的层。例如，这可能是光线从晶片的纹理区域传播到晶片的主体。

下面的图像显示了选择”随机”形态时如何实现这种传播。它们描绘了光线与（i）壁和（ii）单位晶胞底部相交。当光线与这些边界平面之一相交时，它被分配该边界上的新随机位置，然后光线通过公共边界上的相同位置以相同的传播角度传播到相邻单位晶胞（或层）。因此，特征不旋转，而只是相对于彼此平移。

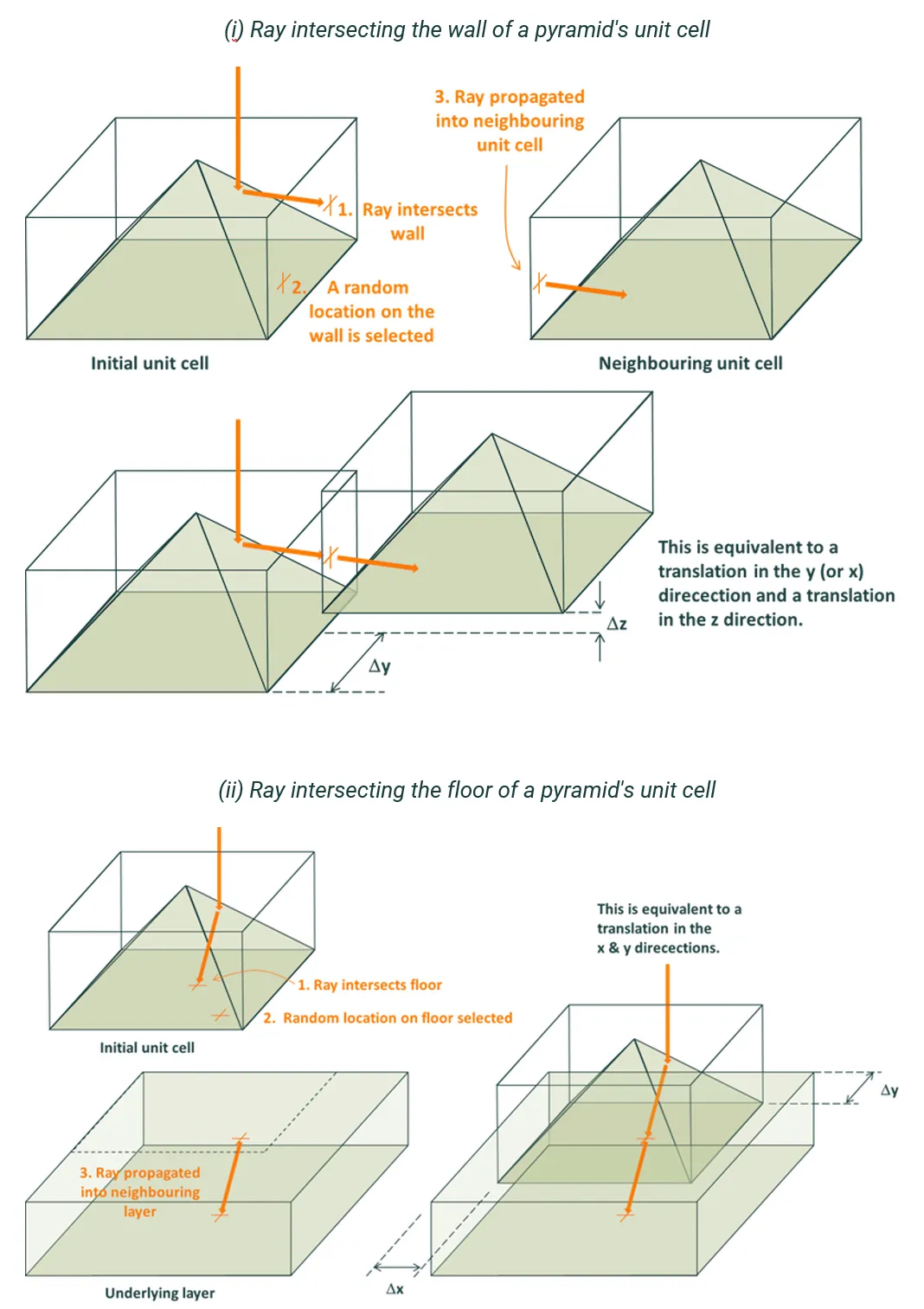用于模拟具有随机形态的单元纹理的光线追踪算法。

散射模型

所有类型的界面都可以有额外的散射。散射用两个选择定义：（1）分布（即散射光的角度分布）和（2）分数（散射光的百分比）。在纹理表面的情况下，散射被定义为发生在纹理的小面上。当在表面施加散射时，SunSolve在光线与表面相互作用后随机化光线的偏振。

散射分布

光学散射由三个模型之一实现：“无散射”、“朗伯散射”或”Phong散射”[Phong75]。这些模型由下面的图表示。

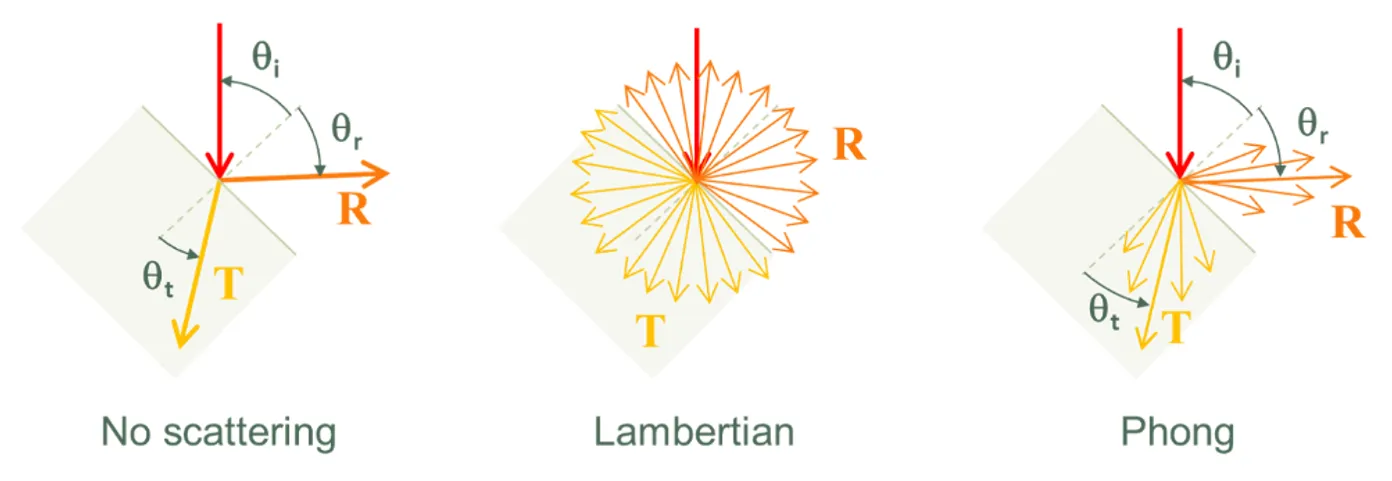光学散射模型。

每当光线与界面相交时，SunSolve首先使用第4.1节中描述的随机方法确定光线是被反射还是被透射。然后SunSolve确定光线的新方向，其中该方向取决于散射模型。在无散射的情况下，光线的新方向通过假设界面是镜面的来确定，因此反射角θr等于入射角θi，透射角θt由斯涅尔定律给出。

朗伯散射

对于朗伯散射，定义光线新方向的球极坐标角（θ和φ）从以下随机确定

$$\theta = \cos^{-1} \left( \chi^{\frac{1}{2}} \right)$$

和

$$\phi = 2\pi\chi$$

其中χ是随机数，0 ≤ χ < 1，并且生成唯一的随机数来确定θ和φ。对于无限多的光线，这些方程导致朗伯反射（或透射），从而每个立体角的光强度是均匀的。请注意，新的光线方向独立于θi。

Phong散射

对于Phong散射，SunSolve将新方向确定为

$$\Delta\theta = \cos^{-1} \left( \chi^{\frac{1}{1+\alpha}} \right)$$

和

$$\phi = 2\pi\chi$$

其中α称为Phong指数，Δθ是新角度与镜面反射之间的差，Δθ = θ – θr，或镜面透射，Δθ = θ – θt，取决于光线是被反射还是被透射。这遵循Schümacher对Phong模型用于随机光线追踪的实现[Schümacher1994]。

因此，当α = 1且θi = 0（正入射）时，Phong散射与朗伯散射相同，当α无限大时，它与”无散射”相同——尽管α = 1,000,000足够高以模拟镜面表面。SunSolve将α限制为1 ≤ α ≤ 1,000,000。

下图显示了概率函数f(Δθ) = (cosΔθ)1+α如何取决于Δθ和α。注意：这不是强度函数。

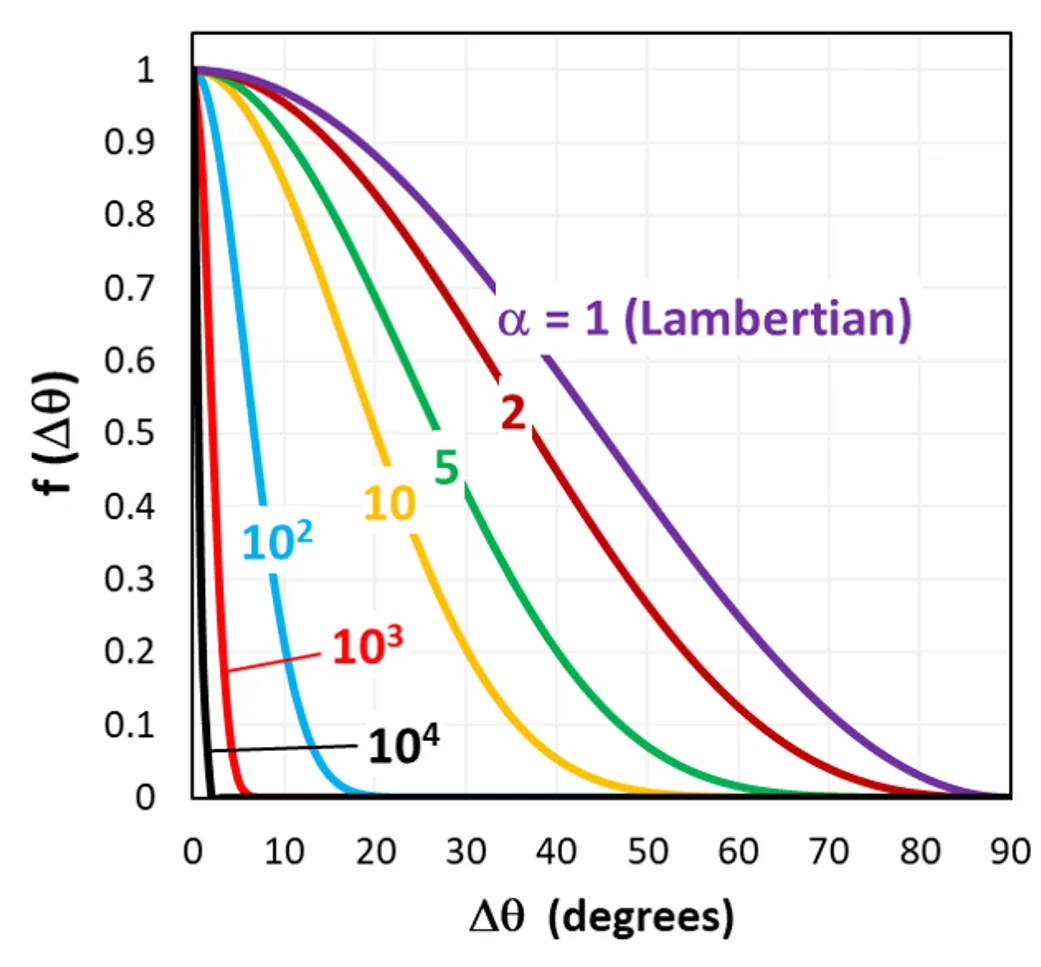Phong散射，显示各种Phong指数值的散射角的归一化角度分布。

请注意，从上图可以看出，Phong散射可用于模拟”聚焦”散射。例如，对于α = 1000，反射光线的散射光将大约为θ = θr ± 5°。这在模拟基角变化± 5°的随机金字塔时可能很有用。

散射分数

有两种计算散射入射光线分数的方法。

第一种方法是设置恒定散射分数Λ。这意味着对于与表面相互作用的每条光线，Λ将被选择的散射模型散射，其余的将不被散射。因此，设置Λ = 0将意味着无论选择什么散射模型，都没有散射。

第二种方法是应用标量散射模型[Carniglia1979][Dominé2010]。使用该模型，散射分数Λ不是恒定的，而是随波长增加而减小。该分数还取决于入射角、材料的折射率以及光线是被反射还是被吸收。该模型旨在近似几何特征尺度与入射光波长相似（例如，黑硅纳米纹理）的表面的响应。

对于反射，

$$\Lambda = 1 - exp \left[ -\left( \frac{2\pi}{\lambda} \cdot \sigma_{rms} \cdot 2 \cdot n_i \cdot \cos\theta_i \right)^2 \right]$$

对于透射，

$$\Lambda = 1 - exp \left[ -\left( \frac{2\pi}{\lambda} \cdot \sigma_{rms} \cdot |n_i \cdot \cos\theta_i - n_t \cdot \cos\theta_t| \right)^2 \right]$$

其中σrms是表面的均方根粗糙度。

下图绘制了散射分数作为波长和σrms的函数，对于入射介质ni = 1.5，其中入射角为θi = 0°（实线）或50°（虚线），由标量散射模型确定。

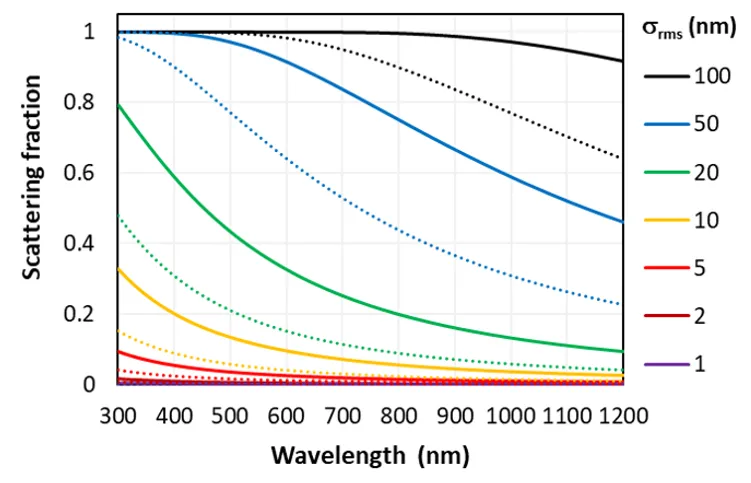散射分数作为波长的函数，由SunSolve内的标量散射实现定义。显示输入sigma的各种值，该值表示表面的均方根粗糙度。