组件电子学

SunSolve Yield使用基于物理的电路方法对光伏组件的完整电气行为进行建模。每个太阳能电池由单二极管等效电路表示，连接在复制组件真实电气布局的网络中——包括串联和并联串、互连和可选旁路二极管。每个电池的光生成电流直接来自光线追踪的光学吸收，而温度相关的电气参数在每个时间步长求解，以确定电流-电压（IV）特性和组件输出。这种方法在模拟中提供了光学、热学和电气域之间一致的、基于物理的联系。

下表提供了组件电子学模型的摘要。

参数	模型	注释	参考文献
电池电流-电压输出特性	带Rs和Rp的单二极管等效电路	光伏行业事实上的标准。有关全面综述，请参阅参考文献。	[Chin2015] [McIntosh2001]
辐照度相关分流电阻	PVsyst辐照度相关分流模型	这主要用于非晶硅器件。	[Mermoud2013] [Mermoud2014]
组件电路	DC SPICE电路	定义并求解组件的完整SPICE模型。	[SPICE3f5]
二极管模型	Level 1 SPICE模型	基于伯克利大学的SPICE 3f5实现	[SPICE3f5]
电池串联电阻的计算	一组解析方程	仅适用于复杂组件。	[Green1982]
电流-电压输出的温度依赖性	PVsyst模型		[Mermoud2014]

太阳能电池的等效电路模型

太阳能电池的等效电路模型如下图所示。它包括光生成电流的电流源、器件内复合的单二极管以及多数载流子电损失的分流和串联电阻器。该电路广泛用于产量建模，以计算电池和组件在各种工作条件下的电气输出。

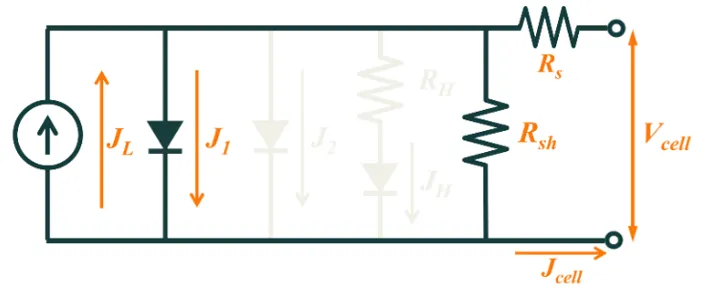太阳能电池的等效电路。

请注意，在SunSolve Yield中，n=2二极管和电阻限制增强复合组件被禁用。这是必要的，因为当前应用的温度模型不考虑它们，并且对于许多光伏组件，确定这些输入所需的完整测量输出集是未知的。¹

IV特性使用以下方程确定：

$$I = I_L - I_0 \left[ \exp \left( \frac{q(V + IR_s)}{nkT} \right) - 1 \right] - \frac{V + IR_s}{R_{sh}}$$

其中I₀、n、*R_s和R_sh*是饱和电流、理想因子、串联电阻和分流电阻的电路输入；全部在标称温度（通常为25°C）下定义。*I_L*是与光线追踪结果相关的光生成电流。

可选地，可以定义辐照度相关分流电阻器。该模型更适用于非晶硅器件，在现代高效组件中，在大多数情况下可能可以忽略。请注意，如果仅为匹配最大功率点的弱光行为而包含此模型，则不清楚该模型的包含如何影响反向偏置行为。

$$R_{sh} = R_{sh,inf} + (R_{sh,0} - R_{sh,inf}) \times \exp \left( -R_{sh,exp} \times \frac{G}{G_{ref}} \right)$$ $$R_{sh,inf} = \frac{R_{sh,ref} - R_{sh,0} \times exp(-R_{sh,exp})}{1 - exp(-R_{sh,exp})}$$

其中G是辐照度，*G_ref*是参考辐照度（通常为1000 W/m2），*R_sh,0*是零辐照度下的分流电阻，*R_sh,ref*是参考辐照度下的分流电阻，*R_sh,exp*是指数（c-Si通常为5.5，其他技术>10）。

组件电路

组件电路包括通过节点点矩阵连接的”连接器”和”电池串”阵列（见下图）。

连接器定义了电池串如何连接在一起，可以是四种类型之一：

• 开路：没有电流流过连接器，两侧的节点电气隔离。

• 短路：无损连接（即电阻 = 0 Ω），电流可以在相邻节点之间流动。

• 旁路二极管：如下文所述的单个SPICE二极管，二极管可以面向任一方向。

• 组件端子：将组件电路连接到外部负载的端点，每个面板必须有一个正端子和一个负端子。

电池串包含从正端子到负端子连接的一个或多个太阳能电池等效电路。电池可以排列成在照明下电流沿任一方向流过串。

已实现三种不同的电路布局：

• 传统c-Si：交替的”连接器”和”电池串”行。该模型可配置以匹配各种c-Si光伏组件。

• 具有返回路径的奇数列：具有包含返回路径的额外列（实现为短路）的奇数个电池串列。这用于对具有较大半切电池尺寸的面板进行建模。

• 水平串：两列”连接器”，中间有一列并联”电池串”。这种布局更常用于薄膜组件，例如FirstSolar CdTe产品。

传统c-Si布局如下所示，它包括交替的连接器和电池串行。至少需要一个电池串和四个连接器。可以在X和Y方向上添加更多电池串。对于添加的每个新列，向每行添加一组新的连接器。请注意，许多外部连接器通常设置为开路。

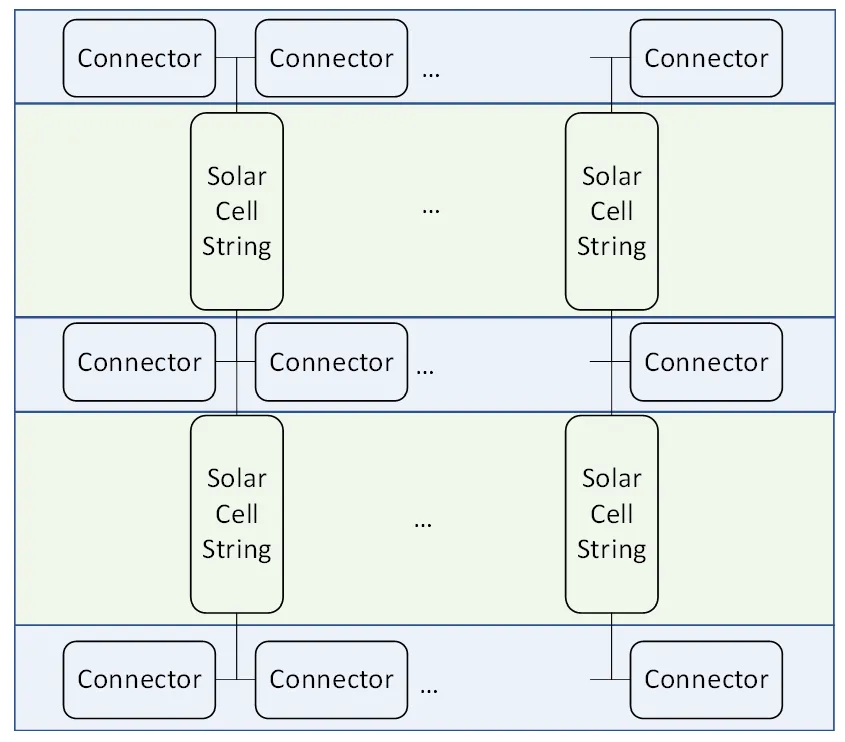“传统c-Si”选项的通用电路布局。矩阵包括交替的连接器和电池串行。

下面显示了两个传统c-Si组件电路的示例。两者都具有用三个旁路二极管连接的并联电池串组。

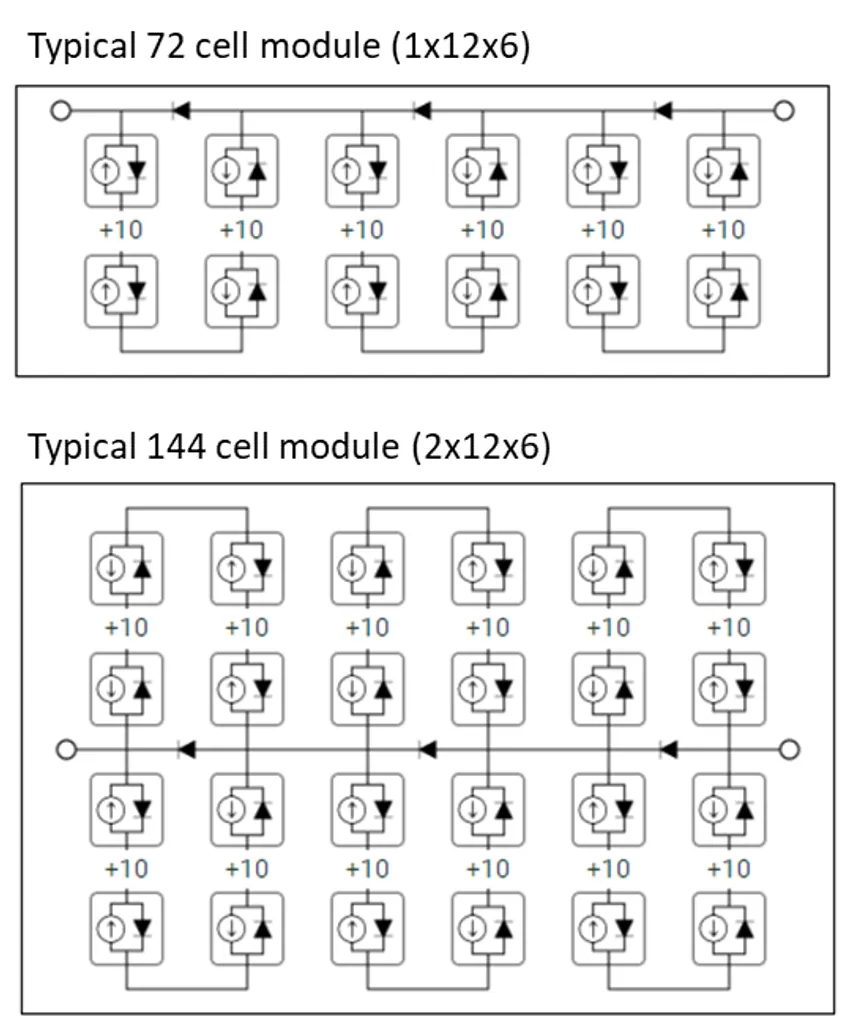“传统c-Si”选项的示例组件电路。

水平串布局如下所示，它包括两列连接器和中间的并联电池串列。至少需要一个串和一对连接器（组件端子）。可以添加具有一对连接器（短路）的新并联电池串作为新行。

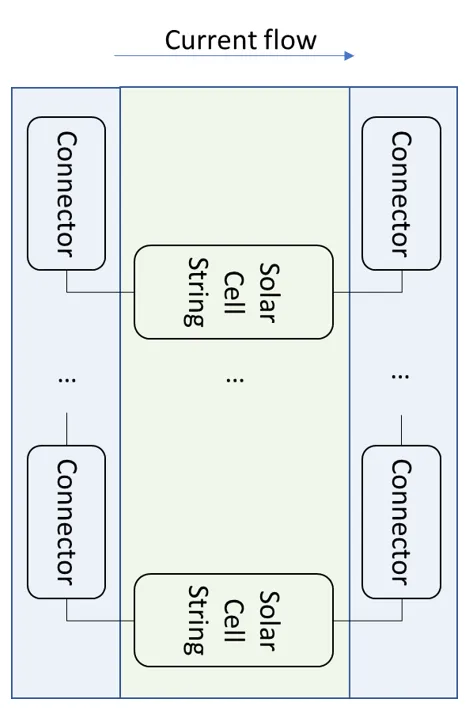“水平串”选项的通用电路布局。矩阵包括两列连接器和中间的并联电池串列。

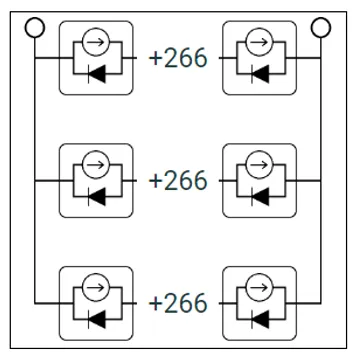“水平串”选项的示例组件电路。在这种情况下，有三个并联串，每个串有268个串联电池。

旁路二极管模型

旁路二极管有两个可用模型，两者都基于用于二极管建模的常见SPICE方法。

“简单”模型没有温度依赖性、没有串联电阻、没有反向击穿。通过旁路二极管的电流（IB）由以下确定：

$$I_B = \begin{cases} I_{S,B} \cdot \left[ \exp \left( \frac{V_{BD}}{N_B V_T} \right) - 1 \right], & V_{BD} > -3 \cdot N V_T \\ -I_{S,B} \cdot \left[ 1 + \exp \left( \frac{3 \cdot N_B V_T}{V_{BD} \cdot e} \right)^3 \right], & V_{BD} \le -3 \cdot N V_T \end{cases}$$

其中*I_S,B*是饱和电流，NB是二极管理想因子。

“SPICE Level 1”模型允许定义R_S,B，这是与二极管串联的欧姆电阻器。它还允许定义”导通拐点”反向偏置击穿电压BV，此时二极管电流转向流动反向偏置击穿”拐点”电流IBV。饱和电流的温度依赖性通过定义带隙电压（EG）和温度指数XTI来实现，如以下方程所示：

$$I_s(T) = I_s \exp \left( \left( \frac{T}{T_{NOM}} - 1.0 \right) \cdot \frac{EG}{N V_T(T)} + \frac{XTI}{N} \cdot \ln \left( \frac{T}{T_{NOM}} \right) \right)$$ $$V_T(T) = \frac{kT}{q}$$

请注意，太阳能组件中的旁路二极管通常在它们通常经历的反向电压范围内没有反向击穿行为，因此BV的值可以设置得很高。

下图演示了将二极管模型拟合到典型太阳能旁路二极管。

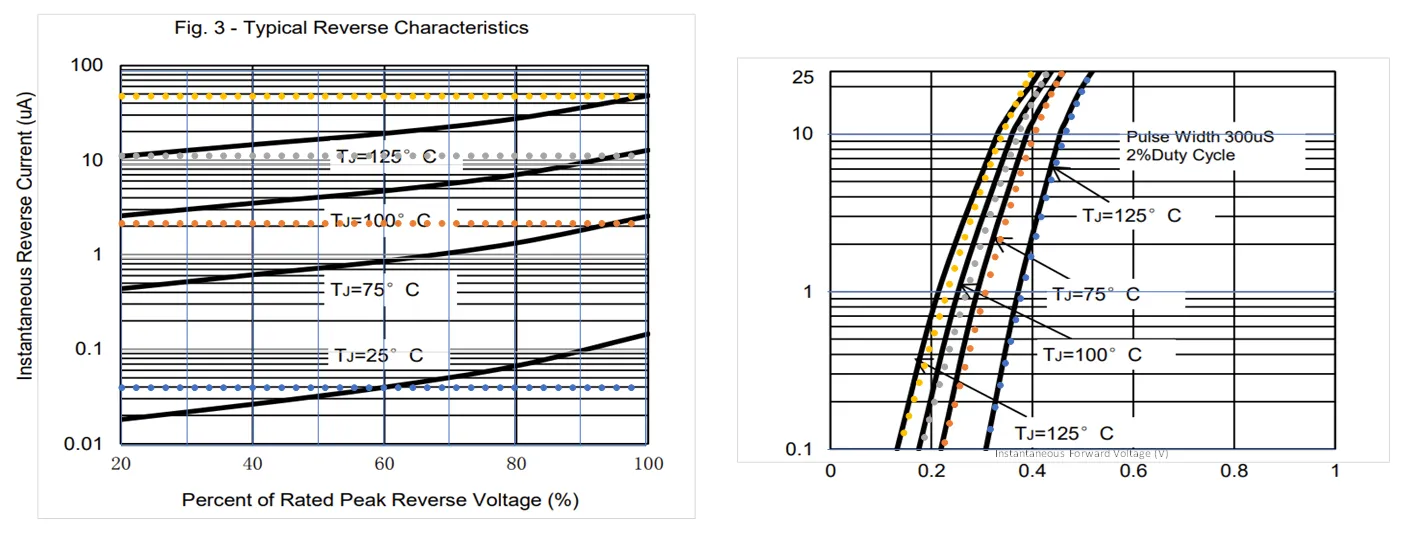使用完整SPICE level 1模型（符号）模拟典型太阳能旁路二极管与数据表上报告的正向（右）和反向（左）二极管特性（线）之间的比较。

电池光生成电流的确定

使用以下程序在每个时间步长计算每个电池内的光生成电流：

1. 基于所选天空模型调整入射辐照度的直射和各向同性分量的波长相关光子计数。

2. 基于最近三个太阳角度的线性插值，为特定太阳位置计算电池内的波长相关吸收。

3. 在每个波长处，将光生成电流的四个分量计算为：

   $$J_{L,front,direct} = \cos(\text{zenith}) \cdot J_{Ph,normal}(\lambda) \cdot A_{front,direct}(\lambda) \cdot SF_{front}(\lambda)$$ $$J_{L,rear,direct} = \cos(\text{zenith}) \cdot J_{Ph,normal}(\lambda) \cdot A_{rear,direct}(\lambda) \cdot SF_{rear}(\lambda)$$ $$J_{L,front,diffuse} = J_{Ph,isotropic}(\lambda) \cdot A_{front,isotropic}(\lambda) \cdot SF_{front}(\lambda)$$ $$J_{L,rear,diffuse} = J_{Ph,isotropic}(\lambda) \cdot A_{rear,isotropic}(\lambda) \cdot SF_{rear}(\lambda)$$

   其中SF是基于量子效率和正面和背面I_SC的STC值应用于简单组件的波长相关缩放因子（如组件电流缩放中所述）。对于复杂组件，这不是必需的。

4. 标称温度（即25°C）下光生成电流的最终值是上述四个分量的总和。

该值随后根据组件温度进行调整，如下所述。

串联电阻的确定

组件内每个电池的串联电阻可以由用户设置为固定值（无电压或温度依赖性）。可选地，对于复杂组件，可以基于一组解析方程计算该值，这些方程考虑：

1. 电池的几何形状，包括形状、尺寸和厚度。

2. 主吸收衬底的电阻率。

3. 正面和背面电极指间的薄层电阻。

4. 电极指与衬底之间的接触电阻，包括计算传输长度以考虑接触下方的薄层电阻强度。

5. 指、母线和带的形状、布局和电阻率。

6. 用于连接到下一个电池的带的额外长度。

方程基于在最大功率点条件下运行时计算组件中的功率损失，然后将其转换为电阻值的方法。Green教授的教科书[Green1982]描述了一般方法以及许多方程。当使用解析方法时，可以添加额外量的串联电阻（R_s，a）以考虑方程中未包含的其他组件，例如组件连接器。

电路的温度依赖性

使用PVsyst电路温度模型[Mermoud2014]确定等效电路输入的温度依赖性。J_L、I₀和n的输入值根据以下进行调整：

$$I_L(T) = I_{L,nominal} \cdot \left( 1 + \left( \frac{\mu_L}{100} \right) \cdot (T - T_{nominal}) \right)$$ $$I_0(T) = I_{0,nominal} \cdot \left( \frac{T}{T_{nominal}} \right)^3 \cdot \exp \left[ \frac{q E_G}{nk} \cdot \left( \frac{1}{T} - \frac{1}{T_{nominal}} \right) \right]$$ $$n(T) = n_{nominal} \cdot \left( 1 + \left( \frac{\mu_n}{100} \right) \cdot (T - T_{nominal}) \right)$$

其中μ_L和μ_n是模型的输入，表示以%/°C测量的I_L和n的变化，Tnominal是I_L、I₀和n的指定参考温度（通常为25°C）。

电池间失配

SunSolve使用以下程序在产量模拟的每个时间步长计算电池间失配。

对于每个组件：

1. 从光线追踪和电池收集效率确定每个太阳能电池中的光生成电流J_L。

2. 如果它们都在自己的最大功率下运行，则确定每个太阳能电池产生的功率（在组件温度下求解单二极管模型）。这些值的总和是$P_{noMM}$

3. 当所有电池按组件布局连接时，确定组件产生的最大功率，包括与电池串并联的旁路二极管（在组件温度下求解组件的SPICE模型）。这给出PMM。

4. 该组件的绝对失配损失为$P_{noMM} - P_{MM}$。

然后，对于单位系统：

5. 绝对电池间失配损失是每个组件损失的总和：$ΣP_{noMM} - ΣP_{MM}$

6. 相对电池间失配损失是$(ΣP_{noMM} - ΣP_{MM}) / ΣP_{noMM}$

Footnotes

1. 造成这种情况的原因在某种程度上是历史性的，与典型数据表上提供的组件IV输出限制可以测量和随后拟合的输出数量有关。通过包含这些额外的电路组件，有太多需要拟合的输入参数，而输出太少。这个问题可以通过温度相关IV曲线矩阵和复杂曲线拟合算法来确定完整输入集来解决。目前这还没有在SunSolve Yield中实现。同时，建议通过建立一组温度和辐照度相关的工作点，然后用单二极管模型拟合这些点，将多二极管电路模型转换为单二极管模型。 ↩