System electronics

The system electronics converts the DC electrical output of the PV modules within the unit-system into the DC output of strings and the AC output of an array. The PV modules from the unit-system can be series connected in different configurations to define one or more strings. These strings can then be connected in parallel to the DC input of an inverter. The parameters of the inverter then determine the DC operating point of the string at each timestep and the subsequent AC output. The array definition also includes an ohmic wiring resistance which is combined with the operating point current to calculate wiring loss.

The output from the system electronics is the AC power delivered at each time step as well as the DC power output of each string and the DC power seen at the input to the inverter.

The table below provides a summary of the system electronics models.

Parameter	Model	Notes	Reference
Module-to-module mismatch	IV curve combination	Calculated as the difference between: (1) the sum of the independent max power output of every module in the string and (2) the string max power point calculated with all modules connected in series.
DC wiring loss	Simple model	Applies the ‘average resistance seen by inverter’ model used in PVSyst	[Mermoud2014]
Inverter efficiency	PVSyst model	Uses linear interpolation to determine efficiency at any DC operating input condition.	[Mermoud2014]
	Sandia model	A parameterised model for inverter efficiency.	[King2007]

Strings of PV modules

Strings are defined as containing a certain number of series connected modules. Each module in the string is linked to a single specific module from within the unit-system and assumes that module’s IV curve. The modules within the unit-system may be linked to as many times as needed.¹ There is no wiring loss defined specifically within the string (other than what is already included within the module). This is rather defined at the array level.

Calculation of DC string IV curve

The DC electrical output of each string is calculated by combining the IV curves of all modules within the string. Note that these IV curves assume the module is at its calculated operating temperature (see Section 8) and already includes losses due cell-to-cell mismatch.

The algorithm to combine the IV curves in series is as follows:

The maximum current (Imax) at 0 V that occurs in any module IV curve from within the string is determined.
A uniform current step (Istep) is calculated as Ilimit divided by the number of positive IV steps (an advanced user input set to 300 by default).
Loop from a target current (Itarget) of -10·Istep to Ilimit incrementing by Istep. At each step, calculate the DC voltage from each module that would result from a module current of Itarget. Module voltage is determined from the discrete IV points of each module IV curve using linear interpolation. If the target is outside the recorded IV points, then it is projected based on the closest two points. Note that this results in 310 total points.
The string voltage (Vstring) at each Itarget is calculated as the sum of all module voltages determined in (3). A string IV curve is constructed from the pairs [Itarget, Vstring].
The maximum power point of the string IV curve is calculated by fitting with a second order polynomial.

Note that it is possible to define multiple string definitions. In this case the output of each string is calculated as described above and the output recorded. At this point in the solving there is no connection between different string definitions, that is defined at the Array level (see next section).

Array

The array is composed of (i) parallel strings of modules, (ii) an inverter, and (iii) associated wiring (including combiner boxes, connectors and other DC components).² It also defines some solving options, such as the model to use for inverter temperature.

Calculation of the array IV curve

The algorithm to combine the string IV curves in parallel is as follows:

The maximum voltage (Vmax) that occurs in any of the parallel string IV curves is determined.
A uniform voltage step (Vstep) is calculated as Vmax divided by the number of positive IV steps (an advanced user input set to 300 by default).
Loop from a target voltage (Vtarget) of 0 V to Vmax incrementing by Vstep. At each step, calculate the DC current from each parallel string that would result from a string voltage of Vtarget. String current is determined from the discrete IV points of each string IV curve using linear interpolation. If the target is outside the recorded IV points, then it is projected based on the closest two points.
The array current (Iarray) at each Vtarget is calculated as the sum of all string currents determined in step (3). An array IV curve is constructed from the pairs [Iarray, Vtarget].
The maximum power point of the array IV curve is calculated by fitting the resulting curve with a second order polynomial.

Calculation of the AC output of the array

The algorithm that calculates the AC output of the array (including the losses) is as follows:

The string IV curves are determined and then combined in parallel to determine the array IV curve. This was described above.
The DC ohmic wiring loss at the array max power point (MPP) is calculated using the array current from step (1) and the global wiring resistance.
1. $\Delta P*{DC \ wiring, \ MPP} = I*{array,MPP} \times R\_{DC,wiring}$
The current, voltage and power at the inverter DC input are calculated. This is effectively the array values at MPP, minus losses in voltage and power caused by the DC wiring resistance:
1. $I*{DC,in} = I*{array,MPP}$
2. $V*{DC,in} = V*{array,MPP} - I*{array,MPP} \times R*{DC,wiring}$
3. $P*{DC,in} = I*{DC,in} \times V\_{DC,in}$
The operating temperature of the inverter is determined (see Section 10.4).
The values of $I_{DC,in}$ , $V_{DC,in}$ and $P_{DC,in}$ are compared to the limits imposed by the inverter model. These limits are applied in the following order:
1. $P_{DC, thr}$ – minimum threshold power
2. $V_{MPPT, min}$ – minimum input voltage for maximum power point tracking (MPPT)
3. $V_{MPPT, max}$ – maximum input voltage for MPPT
4. $I_{PNOM, max}$ – maximum input current limit
After each step in (5) the current, the voltage and power at the inverter DC input are updated. The new values are calculated using the array IV curve adjusted for the DC wiring resistance.³ In some cases, this requires previous constraints to be reimposed, most notably that the power has not dropped below the threshold power level. (Note that the array voltage cannot be increased beyond the array VOC point nor decreased below zero.)
The inverter losses due to these constraints are calculated as the difference in DC power between the array maximum power point and the power at the new operating point.
The AC output power at the inverter is calculated using the voltage and power at the inverter DC input. This step includes the inverter efficiency as described in Section 10.5
The AC output power is compared to the AC power limit of the inverter. Noting that the AC power limit may depend on the inverter temperature. If the calculated power is greater than the limit, then the DC operating point of the array is adjusted. This is achieved by increasing the array voltage and recalculating the values of $I_{DC,in}$ , $V_{DC,in}$ and $P_{DC,in}$ (to account for the DC wiring loss) until the AC output power is acceptable. If this results in the input voltage increasing above the voltage limit (i.e., $V_{DC,in} > V_{max,MPPT}$ ) then the inverter is switched off and the output power becomes 0 WAC.
The clipping loss is calculated as the difference between the DC power of the array at the maximum power point and the DC power of the array after adjustment to meet the power limitation in the previous step. Note that this is a DC power loss.
Once the final operating point of the array is known, the loss due to the DC wiring resistance is recalculated. Often this value is lower than the value calculated at the maximum power point.

Inverter operating temperature

The inverter operating temperature may impact the maximum AC power output. There are three models available to determine the operating temperature of the inverter. These are the same models as used in PVSyst.

“External ambient” – uses the ambient temperature from the weather
$T_{inverter} = T_{ambient}$
“External ambient with shift”
$T_{inverter} = T_{ambient} + T_{offset}$
“Fixed temperature with linear heating”
$T_{inverter} = T_{base} + T_{increase} \cdot (G_{inc,front})$

Where $T_{ambient}$ comes from the weather file, $G_{inc,front}$ is calculated (see Section 8.1) and $T_{offset}$ , $T_{base}$ , $T_{increase}$ are all user inputs.

Inverter conversion efficiency

The inverter conversion efficiency is used to convert the DC input power into AC output power. Depending on the inverter model this may include the impact of the DC operating point (i.e. the DC input voltage and current). There are currently two models that can be used for this. The PVSyst model (for which the inputs are described in an *.OND file) and the Sandia model. Currently (as of February 2025) only the PVSyst model is available to general users.

PVSyst inverter model

The model is implemented as described in [Mermoud2014].

Sandia inverter model

The inverter conversion efficiency can be modelled using the Sandia approach.⁴ It accounts for the self-consumption of power and includes a dependency of the efficiency on DC power and DC voltage.

Some features of SunSolve’s implementation of the Sandia inverter model are as follows:

The model is only available to users that can access advanced options.
Night-time power consumption is included and applied in any hour for which (1) GHI is zero, (2) an ‘error’ occurs during yield solving, or (3) the DC calculation is excluded.⁵
The dependence of inverter efficiency on ambient temperature is neglected.⁶
Temperature-related derating is neglected.⁷
Power clipping is based on both the minimum DC power and maximum AC power.
No voltage or current limitations are enforced.
Table VIII summarises the inputs used to simulate the inverter. The Sandia model provides a parameterisation of the inverter efficiency curve via the set of four coefficients (C0 to C3).

Table VIII: Inverter inputs for simulating field performance [King2007].

Property	Units	Symbol
Number of MPPT
Max AC Power	WAC	PAC0
Max DC Power	WDC	PDC0
Nominal AC voltage	VAC
Nominal DC voltage	VDC
Max DC current	ADC
Max DC voltage	VDC
Min MPPT DC voltage	VDC
Max MPPT DC voltage	VDC
Power use at night	WAC
Power use during operation	WDC	PS0
Sandia 2007 coefficients
curvature of AC output power to DC input power	1/WAC	C0
empirical coefficient allowing PDC0 to vary linearly with DC-voltage input	1/VDC	C1
empirical coefficient allowing PS0 to vary linearly with DC-voltage input	1/VDC	C2
empirical coefficient allowing C0 to vary linearly with dc-voltage input	1/VDC	C3

The AC output power of the inverter when operating (PAC) is calculated using: $P_{AC} = \left[ \frac{P_{AC0}}{A - B} - C \cdot (A - B) \right] \cdot (P_{DC} - D) + C \cdot (P_{DC} - D)^2$ $A = P_{DC0} \cdot [1 + C_1(V_{DC} - V_{DC0})]$ $B = P_{S0} \cdot [1 + C_2(V_{DC} - V_{DC0})]$ $C = C_0 \cdot [1 + C_3(V_{DC} - V_{DC0})]$

The figure below shows how the model simulated within SunSolve compares to the CEC database measurements for an example inverter model.

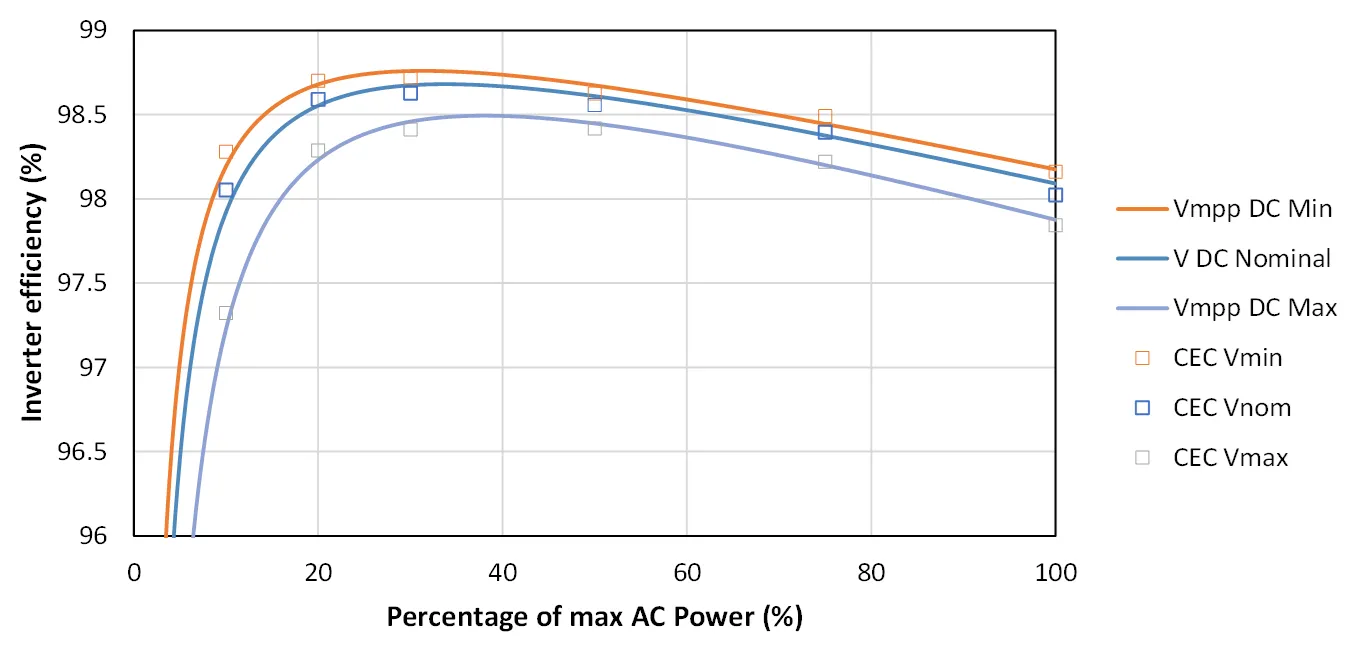SMA SC4000 UP inverter efficiency versus percentage of maximum AC power shown for three different DC voltages (MPPT min, MPPT max and nominal). CEC database measurements are shown as symbols, Sandia 2007 model implementation in SunSolve shown as lines.

For example, if the unit-system represents a single-axis-tracker with a 2P configuration of 56 modules then one string can be defined to contain 28 east (upper) modules and another string to contain 28 west (lower) modules. Additionally, a third string could be defined that contains 14 east and 14 west modules. ↩
Currently the wiring is modelled a single resistance value that accounts for all wiring within the strings, combiner boxes and other components on the DC side. It can be understood as the total resistance seen by the inverter inputs. ↩
For example, if the voltage at the inverter input is lower than Vmin,MPPT, then an iterative solution is used to find the array voltage that, after accounting for the voltage drop across the DC wiring resistance, gives an input voltage to the inverter of Vmin,MPPT. ↩
For a description of the equations see the PV Performance Modeling Collaborative (PVPMC) website: https://pvpmc.sandia.gov/modeling-steps/dc-to-ac-conversion/sandia-inverter-model/ ↩
For example, time steps where the solar zenith is between 88 and 90° are not included in the DC power calculations. ↩
This loss is typically 0.15%abs in inverter efficiency for a 20 °C change in ambient temperature. ↩
This is a protection mechanism implemented in some inverter where they will shut down if they get too hot (to avoid physical damage to the inverter). ↩