Generation profiles

A generation profile describes the generation rate of electron–hole pairs $G$ as a function of depth in the solar cell. Its units are cm⁻³s⁻¹. In SunSolve, $G$ is calculated as a function of distance from both (i) the uppermost point of the solar cell $z$, and (ii) the nearest point on the front surface $\zeta$.

You can enable the solver on the Inputs → Options tab by selecting Generation profiles. This reveals an additional section at the bottom of the input panel where you choose which films and layers are included in the generation profile calculation.

The generation profile is an optional output. SunSolve takes about 2 to 5 times longer to perform the ray tracing when a generation profile is computed, so we recommend that this option is only selected when a profile is actually required.

Z versus Zeta

The following images help explain the difference between $z$ and $\zeta$. The first figure shows how $z$ and $\zeta$ are defined, giving the example of generation occuring at point 1 (in the bulk of the cell) and point 2 (inside a pyramid); the second figure plots contours of $\zeta$ within a textured cell; and the third figure plots $G(z)$ and $G(\zeta)$ for a solar cell when its surfaces are planar (open symbols) or textured with random upright pyramids (closed symbols).

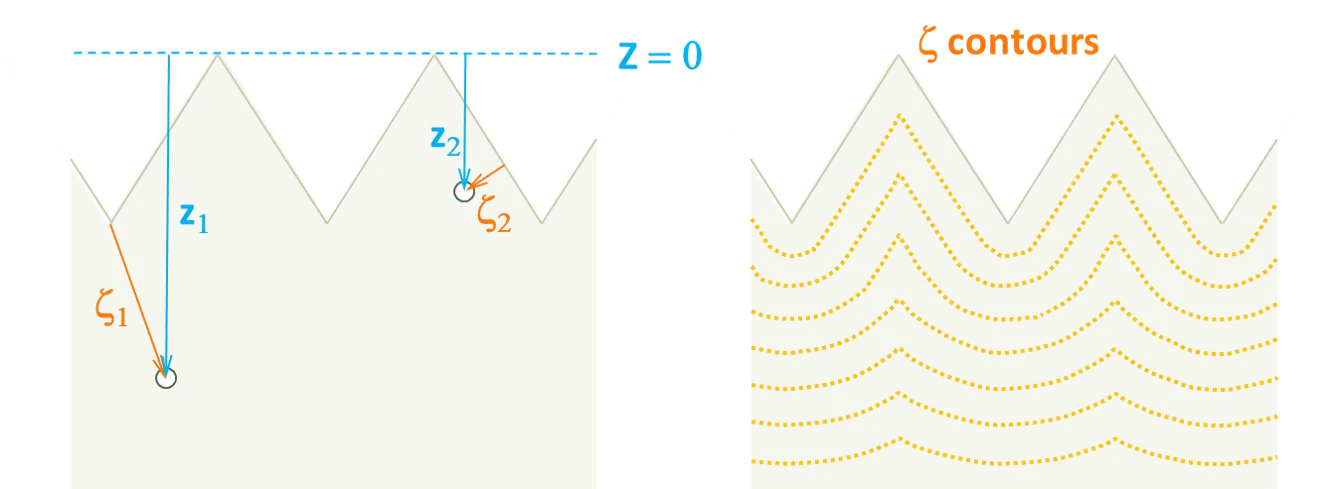
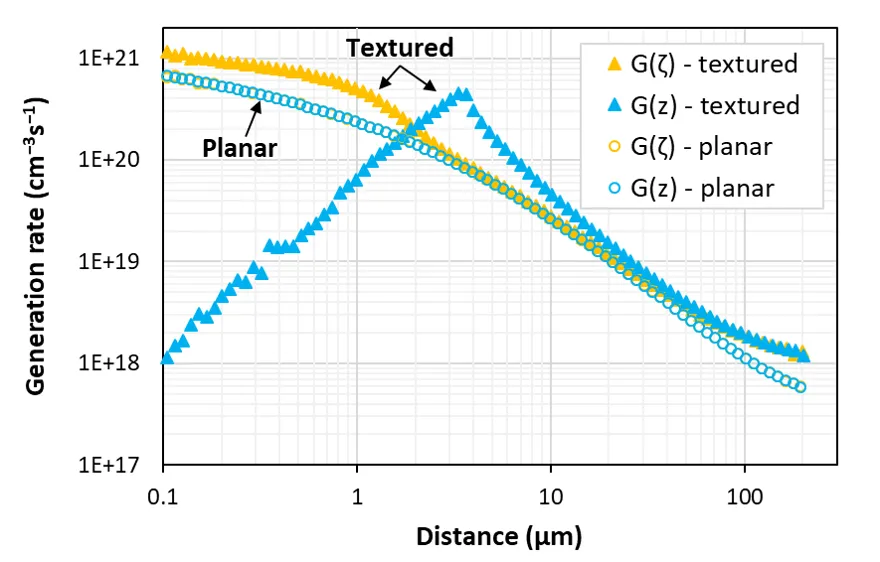
Notice that $G(z)$ and $G(\zeta)$ are identical when the front surface is planar, but different when the front surface is textured.

Also, be aware that $G$ is defined in terms of the cell area (not the local area within the texture). That’s why $G(z)$ decreases with decreasing $z$ when $z$ is less than the height of the pyramids in the textured sample. Although the generation rate might be high within the silicon part of a pyramids, $G(z)$ is here defined over the entire cell area (i.e., it includes the space between the pyramids) rather than just the area contained within the pyramids. The reason we define $G(z)$ this way is so that the integral of $G(z)$ and $G(\zeta)$ are the same and equate to the current density absorbed in the cell $J_{\text{A,cell}}$:

$$\int_{0}^{W}G(z)dz = \int_{0}^{W'}G(\zeta)d\zeta = J_{\text{A,cell}},$$

where $W$ is the thickness of the cell including the height of the front and rear texture, and $W'$ is the thickness of the cell including the height of the rear texture but excluding the height of the front texture. Hence, $W' \leq W$.

The primary purpose of determining $G(\zeta)$ is to convert a 3D problem—such as the generation rate within a pyramid—into a 1D generation profile suitable for semiconductor solvers like PC1D, Quokka and Sentaurus. 1D $G(\zeta)$ profiles are preferable for semiconductor solvers because they are much easier to load than 3D profiles; in most cases they are also sufficiently accurate because minority carriers tend to flow towards the nearest surface to either recombine at the surface or to be collected by a pn junction that is conformal to the surface.